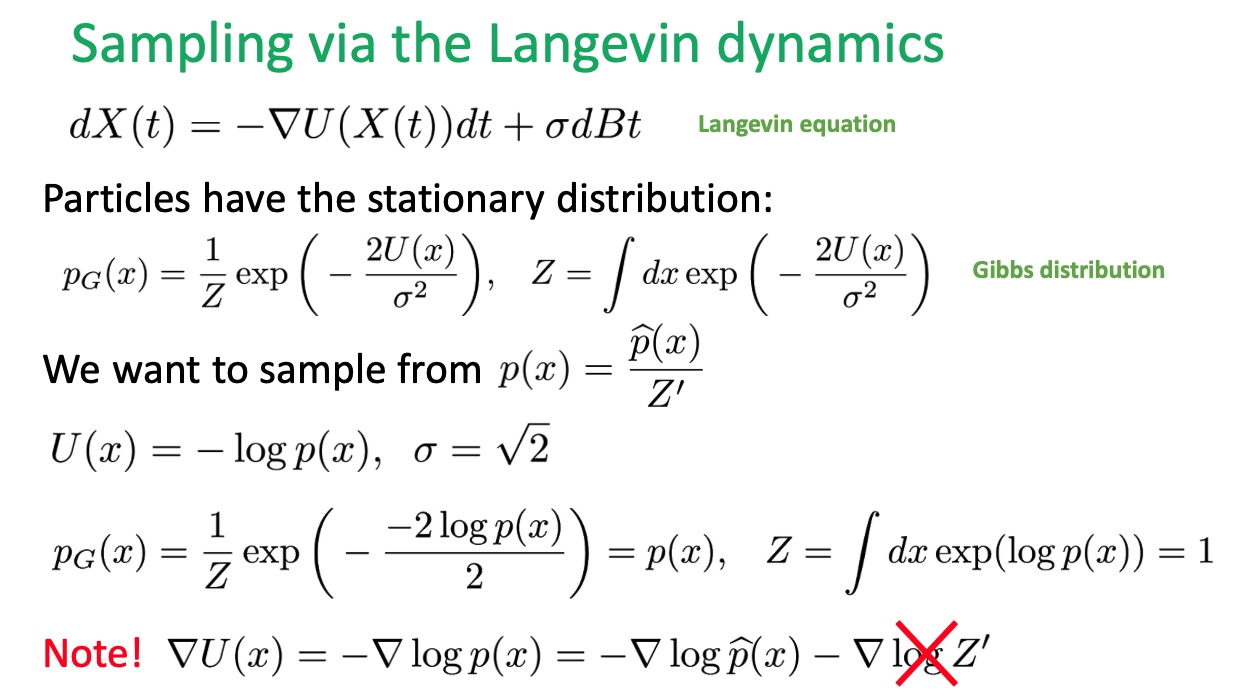基於能量模型（Energy-based model）是一種基於能量函數來定義機率模型的方式，能量函數是用來衡量變數的可能性，為什麼這裡不是說是給出機率呢？因為能量函數的輸出是個實數，能量越小也代表可能性越高，如果要換算成機率就必須要考慮所有的可能性，除上正規化項才能讓這個值符合機率的要求，但求解這個正規化項往往是相當困難的

很多問題其實我們也不用真的去求出正規化項，能量函數已經足夠了，例如分類問題，實際上只需要讓你的目標類別是能量最低的，其他的類別能量提高即可，能量函數的設計相當彈性，所以很多問題其實都可以放入到 EBM 框架裡來解釋，Yann LeCun 大神在最近於 ICLR 2020 也給了個 Keynote 關於 Self-supervised learning 與 EBM 的演講，與YT神人 Yannic Kilcher 線上討論 EBM，還有最近有相當多的基於能量的生成模型，甚至都有超越 GAN 的表現，這經典有點老派的 EBM 最近又熱了起來，趕緊來看看！

Energy-based model

假設我們有一個參數為 $\theta$ 的能量函數 $E_\theta(x)$，將輸入變數$x$輸出一個代表能量的實數，所以可以定義出機率函數為

$$
p_{\boldsymbol{\theta}}(\mathbf{x})=\frac{\exp \left(-E_{\boldsymbol{\theta}}(\mathbf{x})\right)}{Z_{\theta}}
$$

為了要滿足機率的要求，定義正規化項 $Z_\theta$ 為各種可能的 x 下能量的總和

$$
Z_{\boldsymbol{\theta}}=\int \exp \left(-E_{\boldsymbol{\theta}}(\mathbf{x})\right) \mathrm{d} \mathbf{x}
$$

我們可以看到 $Z_\theta$ 是個很難求出的項，因為要把所有 x 的能量都計算出來，在高維度的狀況下是無法被求解的，所以我們需要一些方式來近似或是避免直接去計算 $Z_\theta$

Maximum likelihood training with MCMC

一般來說訓練機率模型的方式就是最大化機率似然值，那我們也來看看如何訓練能量函數的參數$\theta$，來最大化 $p_\theta(x)$，首先來看 $\theta$ 對 $\log p_\theta(x)$ 的梯度如何計算

$$
\nabla_{\boldsymbol{\theta}} \log p_{\boldsymbol{\theta}}(\mathbf{x})=-\nabla_{\boldsymbol{\theta}} E_{\boldsymbol{\theta}}(\mathbf{x})-\nabla_{\boldsymbol{\theta}} \log Z_{\boldsymbol{\theta}}
$$

第一個項就是 $\theta$ 對於能量函數於 x 的梯度，是很容易計算出來的，並沒什麼特別的問題，但第二項我們依然還是有 $Z_\theta$，我們要如何求解 $\nabla_{\boldsymbol{\theta}} \log Z_{\boldsymbol{\theta}}$ 呢？這裡會用上一個計算技巧，計算取 log 的函數 $f$ 的梯度時，可以得到

$$
\nabla_{\theta} \log f(\mathbf{x} ; \theta)=\frac{\nabla_{\theta} f(\mathbf{x} ; \theta)}{f(\mathbf{x} ; \theta)}
$$

應用於 $\nabla_{\boldsymbol{\theta}} \log Z_{\boldsymbol{\theta}}$ 得到

$$
\begin{split}
\nabla_{\boldsymbol{\theta}} \log Z_{\boldsymbol{\theta}}
&= \frac{\nabla_{\boldsymbol{\theta}} Z_{\boldsymbol{\theta}}}{Z_{\boldsymbol{\theta}}} \\
&= \frac{1}{Z_{\boldsymbol{\theta}}} \int \nabla_{\boldsymbol{\theta}} \exp \left(-E_{\boldsymbol{\theta}}(\mathbf{x})\right) d \mathbf{x} \\
&= \int \frac{1}{Z_{\boldsymbol{\theta}}} \exp \left(-E_{\boldsymbol{\theta}}(\mathbf{x}) \right) \left(-\nabla_{\boldsymbol{\theta}} E_{\boldsymbol{\theta}}(\mathbf{x})\right) d \mathbf{x} \\
&= \int \frac{ \exp \left(-E_{\boldsymbol{\theta}}(\mathbf{x})\right) }{Z_{\boldsymbol{\theta}}}\left(-\nabla_{\boldsymbol{\theta}} E_{\boldsymbol{\theta}}(\mathbf{x})\right) d \mathbf{x} \\
&= \int p_{\boldsymbol{\theta}}(x) \left(-\nabla_{\boldsymbol{\theta}} E_{\boldsymbol{\theta}}(\mathbf{x})\right) d \mathbf{x} \\
&= E_{\mathbf{x} \sim p_{\theta}(\mathbf{x})}\left[-\nabla_{\boldsymbol{\theta}} E_{\boldsymbol{\theta}}(\mathbf{x})\right]
\end{split}
$$

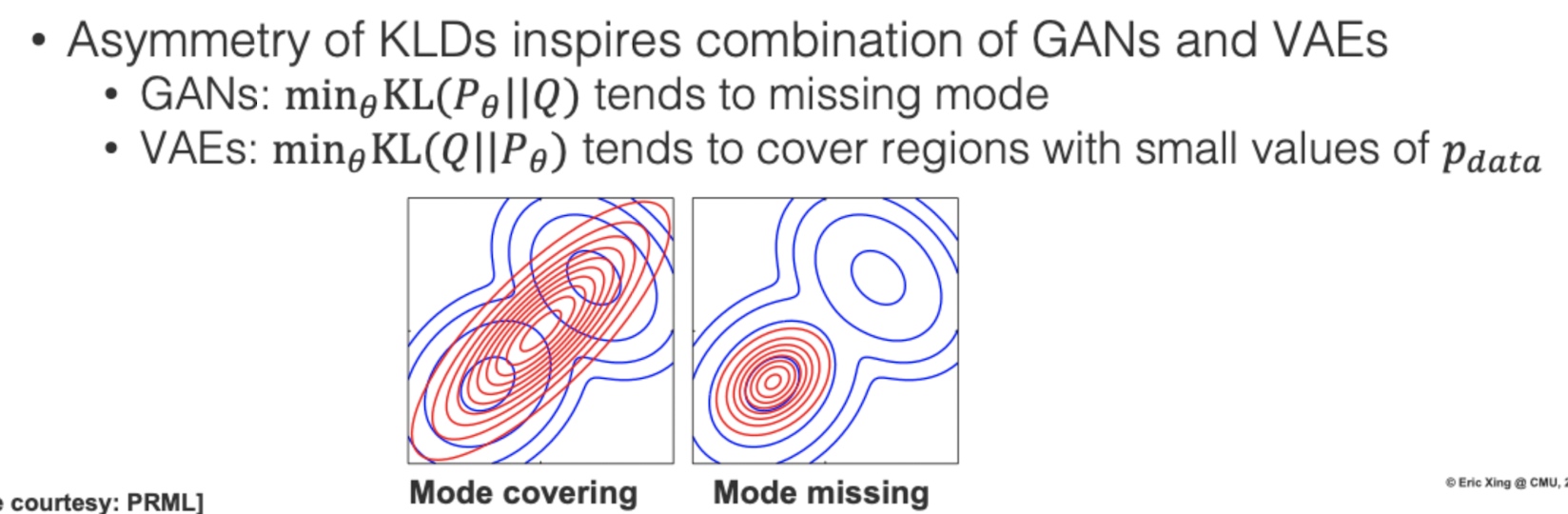
第二項變成我們需要從 $p_\theta(x)$ 抽樣出 x 來計算能量函數的梯度，其實這裡跟 GAN 的訓練過程是有點相似的，如果把判別器看成一種能量函數，就是要對資料給低的能量，而對於抽樣的樣本要賦予高的能量，之後也有一些研究是結合 EBM 與 GAN 的模型，有機會後續會跟大家分享；另外值得思考的是很多基於 MLE 訓練的模型，都只有在資料上學習，但是資料並沒有辦法覆蓋整個空間，這裡除了對資料學習外，還需要去抽樣一些可能的樣本，來增強能量函數的估計能力，這個過程也相似於對比學習 Contrastive Learning，訓練過程中引入負樣本來幫助學習到好的表徵

簡單梳理一下，我們最後得到的式子為

$$
\nabla_{\boldsymbol{\theta}} \log p_{\boldsymbol{\theta}}(\mathbf{x})=-\nabla_{\boldsymbol{\theta}} E_{\boldsymbol{\theta}}(\mathbf{x})- E_{\mathbf{x} \sim p_{\theta}(\mathbf{x})}\left[-\nabla_{\boldsymbol{\theta}} E_{\boldsymbol{\theta}}(\mathbf{x})\right]
$$

Implementation

Colab網址

接著我們來嘗試訓練一個 EBM，這次我使用了 Jax 與 Flax 來實作，最明顯的感受是非常快！可以比我用 Pytorch 的版本快50倍，至於其他的好處與心得，應該會另開一篇跟大家分享，基本上他的語法跟 Numpy 是幾乎相同的，應該是不會影響理解

我們先看一些核心的部分，基本上對應著我們剛推導出來的式子，model 就是我們定義的能量函數，分別對資料與抽樣樣本去計算能量，並計算差異與額外的 regularization

1
2
3
4
5

def loss(param,data,sample):
    pos = model.apply(param,data)
    neg = model.apply(param,sample)
    loss = (neg.mean() - pos.mean()) + 0.1*(pos**2 + neg**2).mean()
    return loss

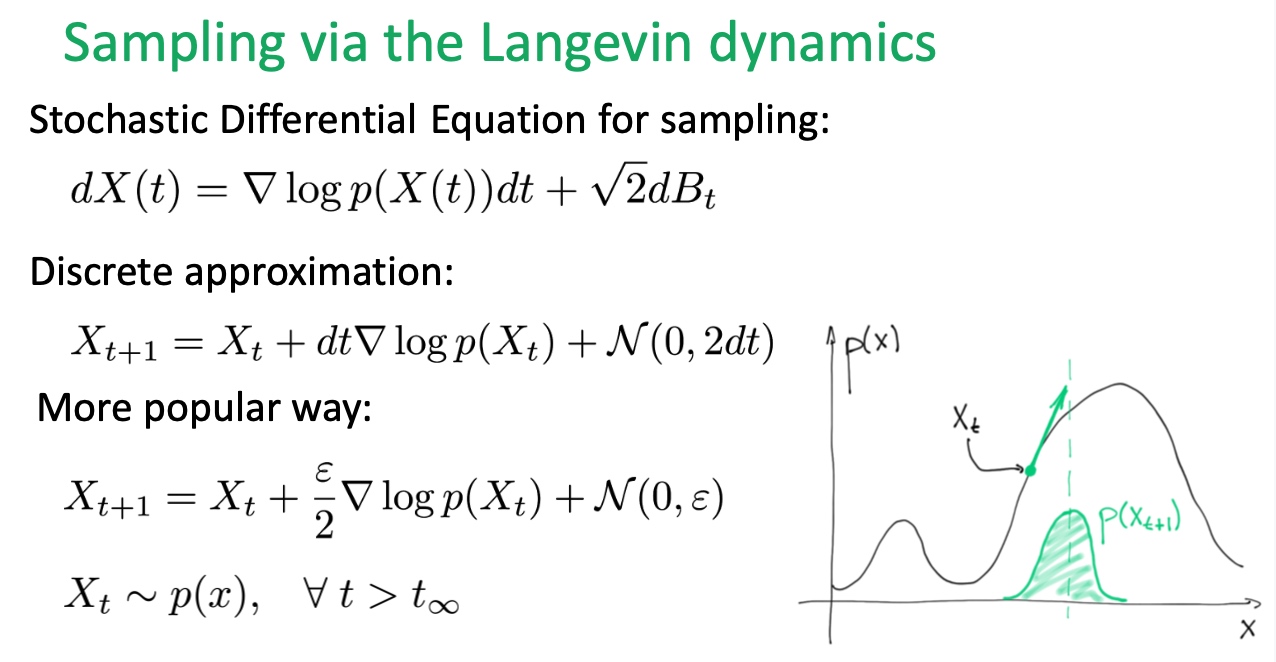
至於如何抽樣出樣本呢？這裡就使用了上一篇介紹的 Langevin Dynamics 抽樣方法，從能量函數中去抽樣出新樣本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

def langevin_sampling(key,
                      init,
                      energy_fn,
                      n_step=20,step_size=1e-2):
    grad_fn = grad(lambda x: energy_fn(x).sum())
    def kernel(carry, noise):
        x, step_size = carry
        grad_x = grad_fn(x)
        x = x + 0.5*step_size*grad_x + jnp.sqrt(step_size)*noise
        return (x, step_size*0.9), x
    
    (x,_),_ = jax.lax.scan(kernel,
                           (init,step_size),
                           random.normal(key,(n_step,) + init.shape))
    return x

可以看程式中的第9行，是對應 langevin sampling 的公式，這裡還有點小技巧就是有加上退火，所以 step_size 會用來越小，抽樣的效果會好很多

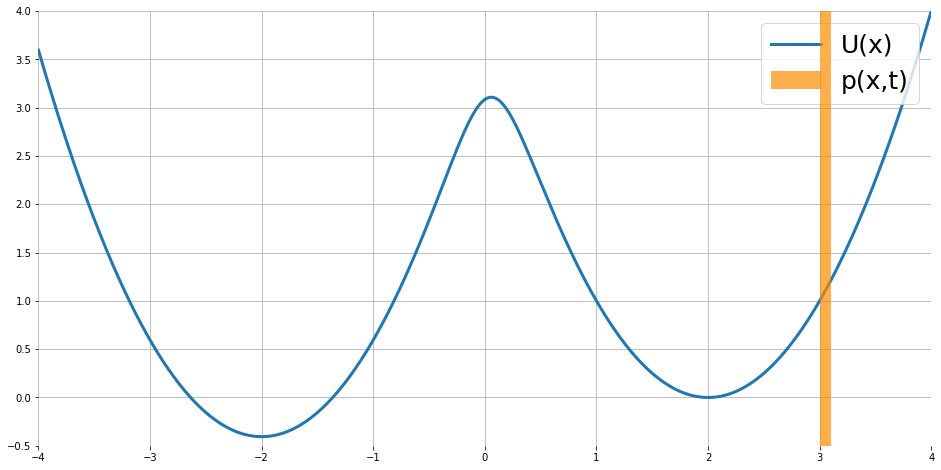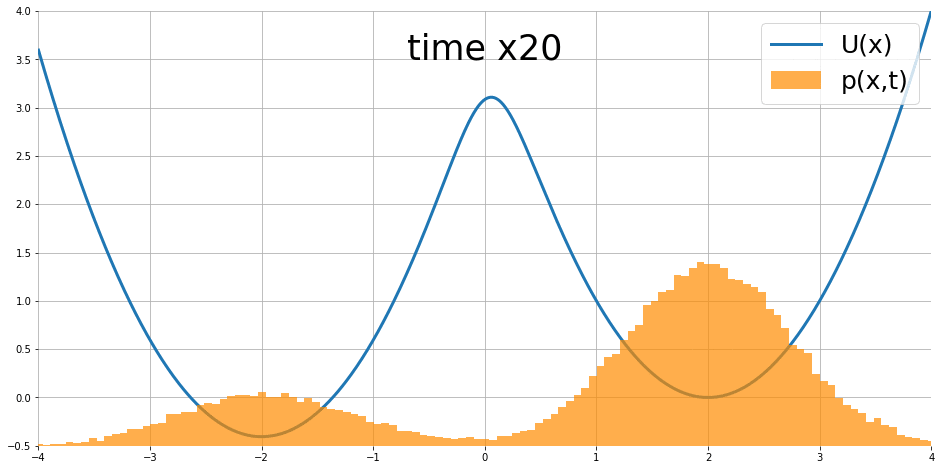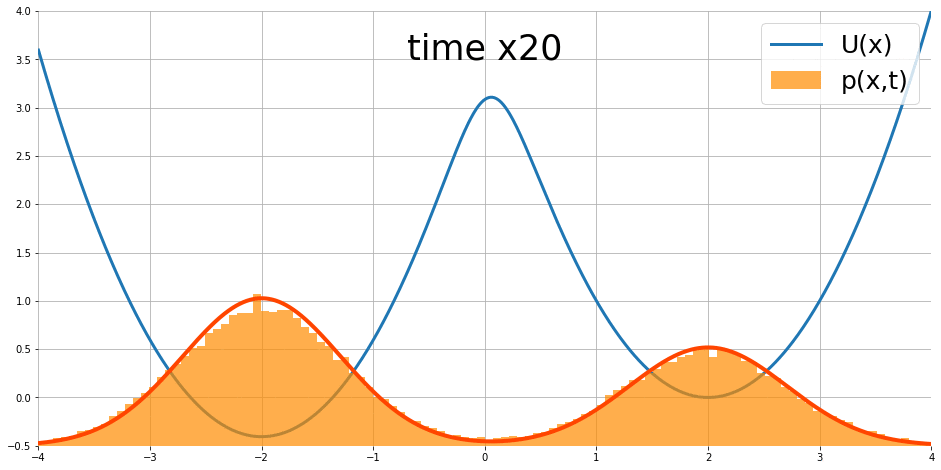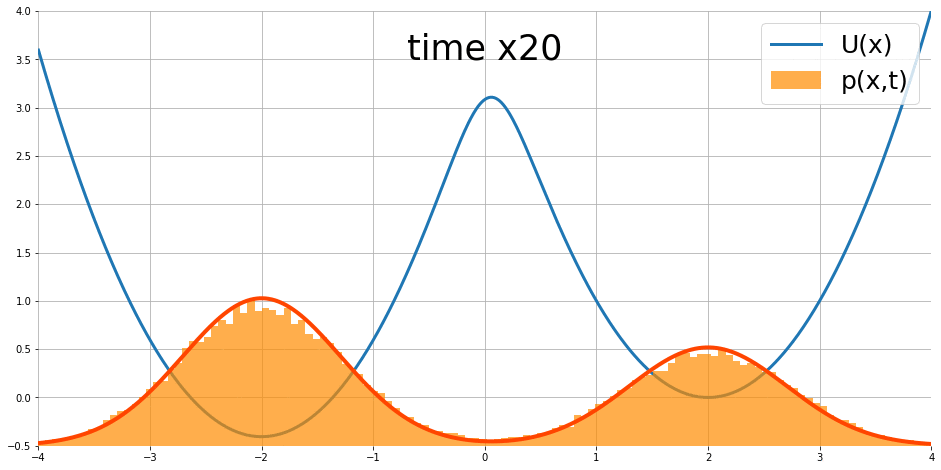
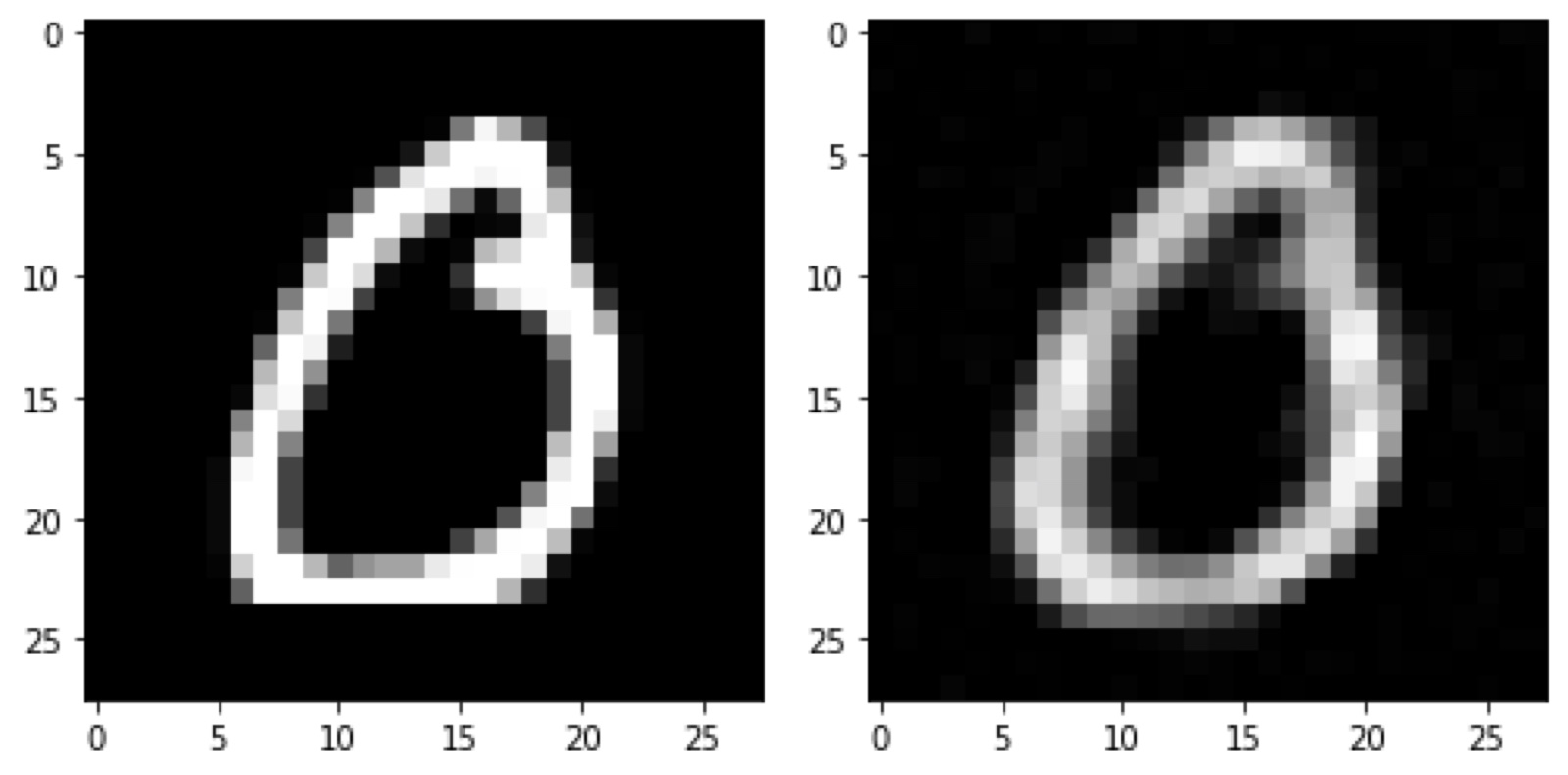
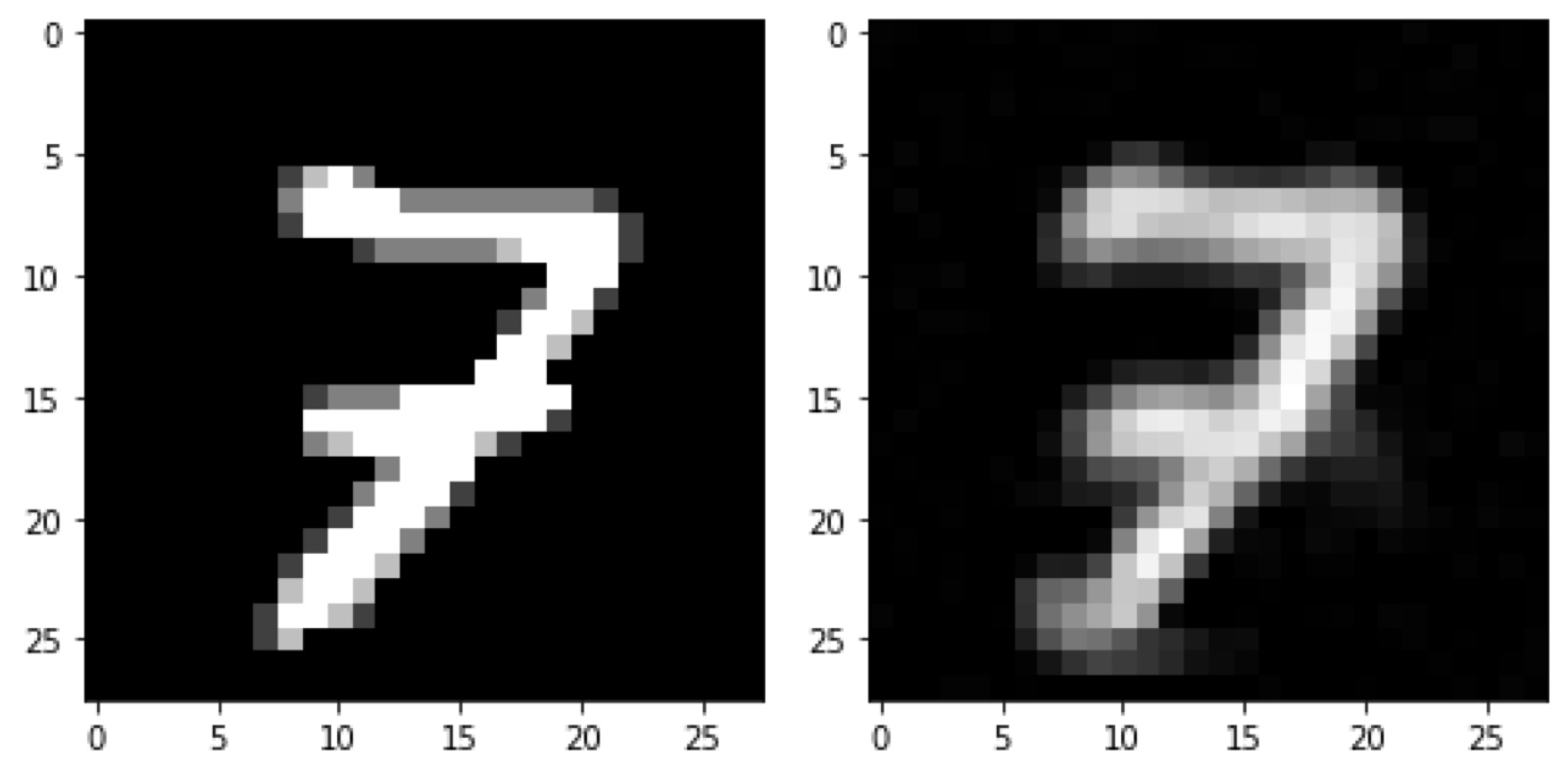
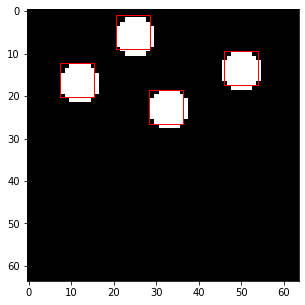
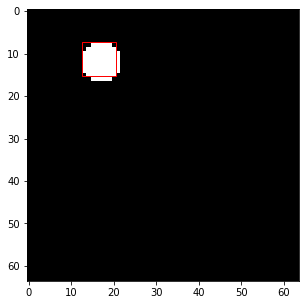
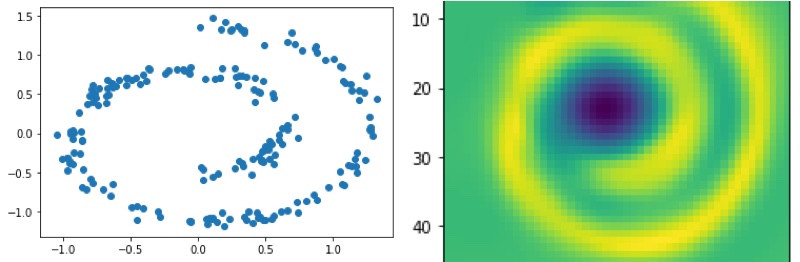
經過訓練後，我們可以看到能量函數有學到資料的分佈（圖有點變形，Colab裡是正常的）

結語

本文章我們了解了 EBM 與如何用 MCMC 方式來訓練，雖然 Langevin Dynamics 已經算是相當快速與好用的一種抽樣方式了，但於更複雜的真實資料可能需要更久的抽樣步數，造成訓練上的難點，而最近相當受到重視的訓練方法為 Score Matching，無需從模型去抽樣來計算梯度，且架構上更適合深度學習模型設計，在影像、三維點雲資料上都有非常驚艷的生成能力，後續我會分享相關的研究，敬請期待！

Refernece

• A Tutorial on Energy-Based Learning
• How to Train Your Energy-Based Models

最近在研究基於能量或是梯度的生成模型，在生成的過程都會需要用到抽樣方法，來從模型學習到的分佈中抽樣出樣本，如何於高維度的空間中抽樣是一個重要問題，例如 Markov chain Monte Carlo 這類演算法，是基於建構一個狀態轉移矩陣來得到一個平穩分佈，最後可以從平穩分佈中來抽樣出樣本，網路上有很多好文章講解 MCMC，雖然在一般常見的深度學習任務中，並不常用 MCMC 來求解積分或是抽樣，但是依然是一個很重要且值得學習的方法

Langevin Dynamics 抽樣方法是另一類抽樣方法，不是基於建構狀態轉移矩陣，而是基於粒子運動假設來產生穩定分佈，MCMC 中的狀態轉移矩陣常常都是隨機跳到下一個點，所以過程會產生很多被拒絕的樣本，我們希望一直往能量低或是機率高的區域前進，但在高維度空間中單憑隨機亂跳，很難抽樣出高機率的樣本，所以如果我們能引入梯度或是一些粒子運動假設，能幫助我們知道高機率的區域應該往哪裡，這樣便可以大幅加速我們抽樣的效率與品質；之前在很多論文中就常看到這個抽樣方法被使用，單看公式非常像梯度下降演算法，只是更新梯度前乘上一個係數並且多加上了一個隨機項，這樣竟然就可以變成一個抽樣方法，優化跟抽樣能一起做，覺得非常神奇，本篇文章是 Langevin Dynamics for sampling and global optimization 的學習心得，底下的圖也都是來自於投影片，但因為內容涉及隨機微分方程，我沒有系統性的學習過，所以僅是整理一下整個 Langevin Dynamics 抽樣方法的概念，數學推導可能不夠嚴謹，如果觀念上有錯誤也請大家不吝指教囉！

Langevin Dynamics

Langevin Dynamics 用隨機微分方程描述了粒子移動，粒子的移動隨著所在位置對能量函數的梯度與隨機項來決定，粒子當下位置$x$可由上一個位置$x’$來形成一個常態分佈所抽樣出來，像是下圖動畫顯示了粒子的運動過程

Fokker-Planck equation

基於上節的運動假設，在某個時間點粒子出現在空間中的的機率，我們可以用 Fokker-Planck equation 來描述，由上一個微小時間點$x’$的位置分佈來計算出特定時間點$x$的位置分佈

$$p(x, t)=\int d x^{\prime} p\left(x, t \mid x^{\prime}, t-d t\right) p\left(x^{\prime}, t-d t\right)$$

粒子的位置分佈會隨時間演化，最終形成一個穩定分佈 (紅色的線)，而這個穩定分佈的樣子跟能量函數有關係

Stationary distribution

我們可以對 Fokker-Planck equation 微分，代表這個機率函數變化的梯度，如果當機率函數不在變化時，也就意指為穩定分佈，求解微分的過程蠻複雜的，用到很多數學技巧，我這邊就不細講，有興趣的人可以自行參考錄影與投影片

第一行就是最後得到的微分公式，我們假設穩定分佈可以寫成 $P_G(x)$，帶入得到的微分公式且當微分為0時，我們就解出 $P_G(x)$裡的 $T$，故之後我們只要知道能量函數 $U(x)$，就可以馬上知道穩定分佈的樣子

Sampling via the Langevin dynamics

我們知道依照 Langevin Dynamics 最終粒子出現的機率會是一個穩定分佈，如果這個穩定分佈恰好是我們設定或是想要的，那穩定後粒子的運動過程就等於抽樣

我們希望從 $p(x)$ 來抽樣出樣本，就是希望穩定分佈最後演化成這樣，我們要讓 $p_G(x) = p(x)$，故得到 $U(x) = - \log p(x)$ 與 $ \sigma=\sqrt{2} $ ，所以帶回去我們的運動假設中

我們終於得到了使用 Langevin dynamics 進行抽樣的方法

結語

本文章我們稍微了解了使用 Langevin dynamics 來進行抽樣背後的原理，雖然抽樣方法可以直接當作工具去使用它，而不用管背後的原理，但是深入理解背後的原理也是相當有趣，很佩服這些受物理啟發的工作，後續我會分享一些生成模型的實作，並使用 Langevin dynamics 抽樣方法，敬請期待！

Refernece

• Langevin Dynamics for sampling and global optimization
• 马尔可夫链蒙特卡罗算法（MCMC）
• Metropolis 蒙特卡罗方法、动力学蒙特卡罗方法、分子动力学方法这三种模拟方法有何特点与差异？

Hinton 大神於2017年提出 Dynamic Routing Between Capsules，探討了CNN的缺陷並提出Capsules概念，2018的 Matrix capsules with EM routing 改進了其中 routing 機制，到2019年這篇 Stacked Capsule Autoencoders 算是這個系列的集大成，概念脈絡更為清楚，大神也在 AAAI 2020 給了一個關於本篇論文的演講，他還特別提到說請大家忘記前兩篇論文，這篇才是對的！足見這一篇論文的重要性

本篇文章不是詳細解讀 Stacked Capsule Autoencoders (SCAE)的文章，如果想要深入了解這篇論文，推薦看第一作者寫的部落格文章與搭配論文服用，本篇文章是想從生成模型的角度去重新理解與實作 capsule 這個概念，建議先閱讀過之前的文章，用生成模型概念來解決物件偵測問題跟本論文也有很相似的概念，另外很有趣的是，上述提到第一作者的部落格文章中，有提到為何不用生成模型的方式來實現 SCAE，這也啟發我一些思考與後續探討，故寫成文章與大家討論

Stacked Capsule Autoencoders

Capsules

在進入模型架構前，想先來談談 capsule 這個概念，上述提到的作者部落格文章中有定義什麼是 capsule

We define a capsule as a specialized part of a model that describes an abstract entity, e.g. a part or an object.

形象上的描述就是積木與組合，一個高階概念是由多個低階概念所組成，低階的概念就像是積木一樣，我們可以組合出更複雜的物件，也就是高階概念，組合的過程中，我們要去選取適當的積木，還要去旋轉積木的姿態來組合；從視覺辨識物件的過程來看，我們看到一個影像並想要知道那是什麼，先去辨識影像用了哪些積木，那些積木分別姿態是什麼，這比起直接去辨識整個物件，積木多半更為簡單，更容易辨識出來，然後我們將有用到的積木搜集起來，看看用這些積木能組合出什麼，透過訓練我們希望特定積木的集合，會對應到特定的物件類別，看到收集到的積木就知道這大概只能組合出哪些東西，我們就能知道這個影像是什麼，這樣組合過程可以一直下去，從只有幾個積木，但到最後可以組合出非常複雜的影像或概念

概覽一下整個模型，輸入影像後找出使用的積木與姿態，再來根據收集到的積木來看能組合出哪些物件

Part Capsule Autoencoder

第一部分訓練模型去學習積木與估計姿態，姿態包含位置、大小、旋轉，積木是指有多個小張影像，例如輸入影像是28x28，積木影像為11x11，輸入影像後模型會輸出每個積木影像的使用機率與姿態，然後還原輸入影像來訓練模型與積木影像

Object Capsule Autoencoder

第二部分為把積木聚合成物件，使用 EM 的迭代估計的方式(類似 Kmean)，來找出中心點，且加入 sparsity regularization 讓積木只集中在某幾個物件上

Implementation

接著我們來嘗試實作 Part Capsule Autoencoder，這個部分與之前實作非監督的物件偵測概念非常類似，也同樣使用 Pyro 來實作，生成模型必須使用積木去組合出影像，積木的使用機率與姿態就是隱藏變量，我們訓練另一個模型去估計這些變量

我的實作於Colab

Model

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

def model(self,obs):
        templates = pyro.param('templates',self.templates)
    
        B = pyro.plate('B',size=self.batch_size,dim=-3)
        N = pyro.plate('N',size=self.n_templates,dim=-2)

        with B,N:
            part_view = pyro.sample('part_view',dist.Normal(self.part_view_prior_mu,
                                                            self.part_view_prior_scale))
            part_logit = pyro.sample('part_logit',dist.Normal(self.part_logit_prior_mu,
                                                            self.part_logit_prior_scale))
  
        layers , imgs_ = self.render(part_view , part_logit)
        imgs = pyro.sample('images',dist.Normal(imgs_ , 0.01*torch.ones_like(imgs_)).to_event(2) , obs=obs)
        return layers , imgs

大致看一下生成模型定義，詳細的函數可以參考我的實作，templates 就是積木，這裡用了16個11x11的影像，並且也是可以學習的，接著每個 templates 都去抽樣出姿態與使用機率，最後用可微分渲染器去生成影像，我們直接生成影像來看看

Result

模型在 MNIST 訓練資料集上訓練，得到一些不錯的結果，下圖左邊是訓練資料，右邊是還原影像

我們來看看模型學到的積木長怎樣，左邊是論文給出的模型訓練在 MNIST 學到的結果，右邊則是實作得到的，雖然與論文設定不完全相同，但顯示模型有學到一些有用的積木

右邊是依照使用機率排序的 templates，左邊是將使用機率高於0.5的積木來組合成影像，顯示模型是會去選擇重要的積木來組成，不是全部都用上

在測試資料集上，也有不錯的效果，右邊是測試資料，左邊是還原影像

選取機率高的積木來組成

結語

我的實作版本與官方實作是不同的，雖然 capsules 概念上是相同的，不同點在於 SCAE 官方實作把 capsules 概念放到估計模型上，而我的版本則放到生成模型裡

• 官方實作：capsules encoder + decoder
• 我的實作：encoder + capsules generator

作者認為 SCAE 當然可以用生成模型來實作，像是我們很熟悉的VI框架一樣，定義一個生成模型與估計模型，用估計模型去近似隱藏變量，但我們往往都是把一些結構先驗知識放到生成模型去，我們會去假設變量之間關係與結構等等，再用任意的模型去當估計模型，但這樣的缺點就是隱變量後驗分佈往往很複雜，估計模型不容易很好近似，估計模型應該需要更多的額外知識來輔助，如果估計模型裡沒有 capsules 架構是無法學到 capsule-like representations 的

我的版本則是照生成模型的概念去實現，如果解碼器太過強大，它是可以忽略編碼器給的訊息，依然可以把資料還原得很好，所以就算編碼器是含有有先驗結構的，也可能無法學到有用資訊，所以我將先驗結構放在生成模型，用估計模型來近似，希望可以得到近似 capsule-like representations 的結果

另外提一個不太嚴謹的想法，我認為人在辨識物件大部分時間都是依賴快速、自動化，接近反射的過程，這是後你用上的是估計模型，是一種快速近似；當你便是不出是什麼物體時候，你會停下來思考，甚至轉動你的視角，嘗試去精確估計，這時候你不會使用估計模型，而是專為你眼前的物體重新去估計變量，經過一些思考計算，你可以精確估計出來積木與姿態等等，並也可以在腦海中還原出這個物體，再把估計到的這些變量丟給估計模型去重新訓練，這裡用的就是監督式學習，估計模型看到這樣的物體就應該要估計出怎樣的變量數值，所以兩種快慢的認知模式，是同時存在與交互訓練的

敬啟期待！

Refernece

• 第一作者的部落格文章
• Stacked Capsule Autoencoders

我們是如何理解由視覺接受到的場景與畫面呢？因為雙眼立體視覺的關係，我們能輕易透過深度感知，來區分遠近背景與物件，個別物件再去理解其位置、描述，甚至是物件之間的關係，我們對於場景的理解是「物件導向」的，我們先有了各種物件的概念，再去感知它們出現在哪？它們有怎樣的描述？它們有什麼關係？腦袋如何生成一幅「心智圖畫」來反應世界？

我們觀測到現實，並且對於其中一些隱藏變量進行估計，例如物件數量、位置、描述等等，然後在腦海中重新生成一幅「心智圖畫」來代表所看到的現實，如果所估計的變量正確，我們期待所生成的心智圖畫會跟現實很像；本篇我們使用 Pyro 來實作一個生成模型，模型生成個別物件的資訊與位置，然後透過可微分渲染器來產生影像，最後使用VI老方法來訓練生成模型與估計模型。

本篇主要參考了 Refernece 中的第一篇，為 AAAI 2019 的論文，簡化了模型與實驗的設定，並且用 Pyro 機率語言更簡明的實作出來（原始論文的code是tf 1.x寫的，很難讀呀…）

我的實作於Colab

可微分渲染器

假設我們有個物件要擺到畫布上，我們可以透過 Indexing，例如array[i,j] = obj，但 Pytorch indexing 是無法傳遞梯度的，例子中的 i,j 是無法微分的，所以我們沒辦法去有梯度改變i,j，把物件移動到我們想要的地方，這可是大問題呀！沒有可微分的渲染器，就沒辦法生成影像，所以可微分程式是很重要的呀！（關於可微分程式之後再跟大家分享討論）

我們希望擺的位置是可以微分的，該怎麼做呢？我們可以用 Spatial transformer networks (STN) 來將物件放到畫布上，並且整個過程是可以微分的，但這裡不詳述STN的原理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def render(obj_param,logit):
  img_param = obj_to_image_param(obj_param)
  img_param = img_param.view(-1,2)
  bs = img_param.size(0)
  
  logit = (logit_scale*logit.view(-1,1,1,1)).sigmoid()
  obj = torch.ones((bs,1,obj_size,obj_size))*logit
  
  theta = torch.zeros(bs,2,3)
  theta[:,0,0] = ratio
  theta[:,1,1] = ratio
  theta[:,:,-1] = img_param
  
  grid = affine_grid(theta, torch.Size((bs,1,img_size,img_size)))
  out = grid_sample(obj, grid)
  out = out.view(batch_size,-1,1,img_size,img_size)
  return out , out.sum(1)

obj_param 代表物件的座標參數，logit 代表物件出現的機率，透過 obj_to_image_param 做參數的轉換，把物件參數轉換到畫布參數，並放到 theta 中用 affine_grid 與 grid_sample 函數來把物件放到畫布上

1

out , img_ = render(torch.zeros(2,4,4,2,2),torch.ones(2,4,4,2,1))

借鏡 Yolo 模型，把影像分成4*4的方格，每個方格內可以有2個物件，每個物件有x,y偏移座標與出現機率，測試一下渲染器，每個方格內有2個白色物件，且偏移座標為0（所以在正中間重疊），出現機率都是1

Yolo-like generative model

模型根據定義的維度，每個物件可能出現的方格內抽樣物件的座標與機率，用Pyro來表示相當簡潔，plate代表每個維度間互相獨立，抽樣出來的參數在送給宣染器來產生抽樣出影像

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def model(obs):
  B = pyro.plate('B',size=2,dim=-5)
  H = pyro.plate('H',size=4,dim=-4)
  W = pyro.plate('W',size=4,dim=-3)
  N = pyro.plate('N',size=2,dim=-2)

  with B,H,W,N:
    pos = pyro.sample('obj_param',dist.Normal(torch.zeros(2),torch.ones(2)))
    logit = pyro.sample('obj_logit',dist.Normal(torch.tensor(-1.),torch.ones(1)))
    
  out , imgs_ = render(pos,logit)
  imgs = pyro.sample('images',
                     dist.Normal(imgs_ , 0.01*torch.ones_like(imgs_)).to_event(2) , obs=obs)
  return out , imgs

從模型直接做抽樣，物件的深淺反映可能出現的機率

Guide

接著來做估計，可以先嘗試看看點估計，看看VI方法能不能估計出想要的隱藏變量

1

guide = AutoDelta(pyro.poutine.block(model, expose=["obj_param","obj_logit"]))

或是用Amortized inference，引入一個估計模型訓練神經網路直接去預測隱藏變量

1
2
3
4
5
6
7
8
9
10
11
12
13
14

encoder = nn.Sequential(nn.Conv2d(1,16,3,2,1),
                        nn.ReLU(),
                        nn.Conv2d(16,32,3,2,1),
                        nn.ReLU(),
                        nn.Conv2d(32,32,3,2,1),
                        nn.ReLU(),
                        nn.Conv2d(32,16,3,2,1),
                        nn.ReLU(),
                        nn.Conv2d(16,6,1,1))
def guide(imgs):
  pyro.module("encoder", encoder)
  feats = encoder(imgs).permute(0,2,3,1).view(batch_size,H,W,C,3).contiguous()
  s1 = pyro.sample('obj_logit',dist.Delta(feats[:,:,:,:,:1]))
  s2 = pyro.sample('obj_param',dist.Delta(feats[:,:,:,:,1:]))

Inference

當 Model 與 Guide 都定義好後，就用VI方法來訓練囉！（比自己從頭寫，方便多了呀！）

1
2
3
4
5
6
7
8

pyro.clear_param_store()
elbo = Trace_ELBO()
optim = pyro.optim.Adam({'lr': 1e-3})
svi = SVI(model, guide, optim, loss=elbo)

for _ in range(1000):
  loss = svi.step(imgs)
print(loss)

Result

把訓練過後的 guide 所估計的物件框畫在訓練資料上來看看，可以看到還蠻不錯的

1
2
3
4
5
6
7
8
9
10

idx = 0
filter_img_param_ = get_bbox(obj_param_[idx],obj_logit_[idx],t=0.5)

plt.figure(figsize=(5, 5))
plt.imshow(imgs[idx].view(img_size,img_size).detach().numpy(),cmap='gray')
currentAxis=plt.gca()
for p in filter_img_param_:
  x,y = param_to_px(p)
  rect=patches.Rectangle((x-5, y-5),obj_size,obj_size,linewidth=1,edgecolor='r',facecolor='none')
  currentAxis.add_patch(rect)

目前我們是直接用模型來生成訓練資料，生成的資料完全符合模型假設，當然比較容易訓練，我們來換個生成訓練資料的方式，用均勻分布的方式抽樣物件數量與位置，還有把物件換成圓形

1
2
3
4
5
6
7
8
9
10

def draw_sprites():
  img = Image.new('L', (64, 64))
  drawer = ImageDraw.Draw(img)
  num_sprite = randint(1,5)

  for i in range(num_sprite):
    x = randint(0,img_size - obj_size)
    y = randint(0,img_size - obj_size)
    drawer.ellipse((x,y,x+obj_size,y+obj_size),fill=(255))
  return img

經過訓練後結果

結語

本篇介紹了一個 Unsupervised object detection 的方法，我們定義了一個影像生成的過程與模型，我們假設所看到的影像背後都有一些隱藏的生成參數，我們如果能很好的估計出來，就能也生成出接近一樣的影像（影像還原誤差），所以我們可以透過著個方式，來評斷估計的隱變量好壞，進而去訓練估計模型預測隱變量，物件座標也只是其中的一種隱變量，還有物件大小、類別、甚至光影都可以是，都可以套用這個框架去延伸，當然本篇只是淺嚐而止，只是一個概念驗證，離能真的用在真實影像上的物件偵測還非常的遠，但多少能換個思路去理解生成模型或是非監督式學習能怎樣扮演其他學習任務的基石。

下篇已經大概知道要寫什麼，但還沒寫之前都不敢說，敬請期待！

Refernece

• Spatially Invariant Unsupervised Object Detection with Convolutional Neural
  Networks
• Attend, Infer, Repeat: Fast Scene Understanding with Generative Models
• Attend Infer Repeat - Pyro

沒想到一晃眼就是一年了，但自己挖的坑還是要填完，希望又能開始恢復寫部落格的習慣，也把自己關注的研究陸續整理上來，期待能獲得一些新想法，要訓練自己能用多個角度去看同一個問題，能把多個問題歸納成同一個框架

本篇是漫談 Variational Inference 系列第三篇，第二篇介紹了VAE，把深度學習與VI做個結合，也引領出了很多後續的研究；而本篇來談談VI方法跟一些其他生成模型的關係，用一致的框架來討論VAE與GAN

New formulation of VAE

首先我們有 $q_{\phi}(x,z)=q_{\phi}(z|x)p(x)$ 與 $p_{\theta}(x,z)=p_{\theta}(x|z)p(z)$，那來對上一篇VAE的ELBO計算期望值

$
\begin{split}
E_x \left[
E_{q_{\phi}(z|x)}
\left[ \log \frac{p_{\theta}(x,z)} {q_{\phi}(z|x)}\right]
\right] &= E_{q_{\phi}(x,z)}
\left[ \log \frac{p_{\theta}(x,z)} {q_{\phi}(z|x)}\right] \\
&= E_{q_{\phi}(x,z)}
\left[ \log \frac{p_{\theta}(x,z)} {q_{\phi}(z|x)} + \log p(x) - \log p(x) \right] \\
&= E_{q_{\phi}(x,z)}
\left[ \log \frac{p_{\theta}(x,z)} {q_{\phi}(x,z)} + \log p(x) \right] \\
&= KL(q_{\phi}(x,z) || p_{\theta}(x,z)) + C
\end{split}
$

做了一些變換後，可以把ELBO表示成兩個聯合機率分布的KL距離，我們關注的是 $p_{\theta}(x,z)$，希望可以生成很真實的樣本，KL是個非對稱的divergence，交換位置是完全不同的效果，生成器$p_{\theta}(x,z)$於計算KL的位置會影響優化的目標，這也導致了VAE生成樣本比較模糊，但不容易Mode collapse的原因，我們接著來看GAN的形式如何，再來一起討論其異同

New formulation of GAN

接著我們也是看看把GAN整理成類似的形式，方便後續的分析比較，$y$代表真實資料(y=1)或是生成樣本(y=0)，現在我們換個角度來看，把$x$當作隱變量而$y$視為可觀測的輸入，我們想用一個候選分佈$p_{\theta}(x|y)$，希望去優化$q_{\phi}(y|x)$這個條件機率(判別器)，GAN訓練過程我們會輸入真實資料與生成樣本給判別器去，我們現在的候選分佈應該是由$g_{\theta}(x)$生成與$p_{\text data}(x)$混合而成，所以把$p_{\theta}(x|y)$寫成：

$$
p_{\theta}(x | y)=\left \{
\begin{array}{ll}
{p_{g_{\theta}}(x)} & {y=0} \\
{p_{\text {data}}(x)} & {y=1}
\end{array}\right.
$$

優化的目標也會依訓練過程不同，兩個階段是相反的，候選分佈會隨機給真實資料或是生成樣本，訓練$q_{\phi}(y|x)$判別器分類正確

$$
\max_{\boldsymbol{\phi}} L_{\phi} = \mathbb{E}_{p_{\theta}(\boldsymbol{x} | y)p(y)}\left[\log q_{\phi}(y | \boldsymbol{x})\right]
$$

於訓練$g_{\theta}(x)$生成器階段，我們希望$q_{\phi}(y|x)$分類錯誤，$q_{\phi}^r(y|x)$表示相反的$y$，優化目標變成

$$
\max_{\boldsymbol{\theta}} \mathcal{L}_{\theta}=\mathbb{E}_{p_{\theta}(\boldsymbol{x} | y) p(y)}\left[\log q_{\phi}^r(y | \boldsymbol{x})\right]
$$

跟VAE不同，兩個階段優化的目標並不一樣，這也導致訓練更為困難，我們對訓練生成器階段做個推導整理，並且加上負號來改成最小化

$
\begin{split}
E_{p(y)}\left[
E_{p_{\theta}(x|y)}
\left[ - \log q_{\phi}^r(y | x)\right]
\right] &= E_{p(y)p_{\theta}(x|y)}\left[ \log \frac{q_{\phi}^r(y | x)p_{\theta^\prime}(x)}{p_{\theta}(x|y)p(y)} - \log \frac{p_{\theta}(x|y)p(y)}{p_{\theta^\prime}(x)} \right] \\
&= KL(p_{\theta}(x,y) || q_{\phi}^r(x,y)) - KL(p_{\theta}(x,y) || p_{\theta^\prime}(x))
\end{split}
$

推導過程中我們加入$x$的先驗分佈$p_{\theta^\prime}(x)= \sum_y p_{\theta^\prime}(y|x)p(y)$，訓練生成器時候，我們會由上一輪訓練出來的$g_{\theta^\prime}$生成樣本與真實資料去訓練新的$g_{\theta}$，所以每次先驗分佈都在改變，最後我們得到一個跟VAE類似的結果，但是$p_{\theta}(x,y)$在KL中的位置是相反的

Compare VAE and GAN

Mode covering and collapse

我們看到兩種模型的優化目標是相反的KL divergence，VAE傾向去覆蓋整個分佈，但也可能會覆蓋到一些機率密度低的位置，而使得有時候抽樣出來的影像不夠真實，所以VAE除了使用L2 loss去計算影像還原損失，本身就會導致模糊外，更深一層本質上是KL的特性所導致

GAN則為相反，傾向去學好一個Mode，認真顧好一個部分就好，所以能產生非常真實的資料，但會有Mode collapse

Different prior

推導過程中我們都有引入$x$的先驗分佈，

• VAE：$p(x)$代表的是真實資料分布
• GAN：$p_{\theta^\prime}(x)$代表的是混和分佈

Mixed prior

我們換從訓練判別器階段來分析，我們嘗試把$p_{\theta^\prime}(x)$當作先驗分佈引入在拆解$q_{\phi}(x,y)$時

$
\begin{split}
KL(p_{\theta}(x,y) || q_{\phi}(x,y))
&= \int p_{data}(x) \log \frac{p_{data}(x)}{q_{\phi}(x,y=1)} + \int p_{g_{\theta}}(x) \log \frac{p_{g_{\theta}}(x)}{q_{\phi}(x,y=0)} \\
&= \int p_{data}(x) \log \frac{p_{data}(x)}{q_{\phi}(y=1|x)p_{data}(x)} + \int p_{g_{\theta}}(x) \log \frac{p_{g_{\theta}}(x)}{q_{\phi}(y=0|x)p_{g_{\theta}}(x)} \\
&= \int p_{data}(x) \log \frac{1}{q_{\phi}(y=1|x)} + \int p_{g_{\theta}}(x) \log \frac{1}{q_{\phi}(y=0|x)} \\
&= E_{p_{data}(x)}\left[ \log D(x) \right] + E_{p_{g_{\theta}}(x)}\left[ \log (1-D(x)) \right]
\end{split}
$

我們得到跟原始GAN paper上熟悉的式子！

Data prior

用变分推断统一理解生成模型（VAE、GAN、AAE、ALI）By 苏剑林文章中引入了$p(x)$當作先驗分佈，一開始不太理解文章與原始GAN的關係，後來經過一番梳理，發現原來只是先驗分佈的不同

$
\begin{split}
KL(p_{\theta}(x,y) || q_{\phi}(x,y))
&= \int p_{data}(x) \log \frac{p_{data}(x)}{q_{\phi}(x,y=1)} + \int p_{g_{\theta}}(x) \log \frac{p_{g_{\theta}}(x)}{q_{\phi}(x,y=0)} \\
&= \int p_{data}(x) \log \frac{p_{data}(x)}{q_{\phi}(y=1|x)p_{data}(x)} + \int p_{g_{\theta}}(x) \log \frac{p_{g_{\theta}}(x)}{q_{\phi}(y=0|x)p_{data}(x)} \\
&= \int p_{data}(x) \log \frac{1}{q_{\phi}(y=1|x)} + \int p_{g_{\theta}}(x) \log \frac{1}{q_{\phi}(y=0|x)} + \int p_{g_{\theta}}(x) \log \frac{p_{g_{\theta}}(x)}{p_{data}(x)} \\
&= E_{p_{data}(x)}\left[ \log D(x) \right] + E_{p_{g_{\theta}}(x)}\left[ \log (1-D(x)) \right] + KL(p_{g_{\theta}}(x) || p_{data}(x))
\end{split}
$

實務上，我們訓練生成器都只去優化第二項，引入Data prior後，整個優化項變成

$$
\mathbb{E}_{p_{g_{\theta}}(x)}\left[ \log (D(x)) \right] + KL(p_{g_{\theta}}(x) || p_{data}(x))
$$

我們假設$p_{data}(x)$可以由上一輪的$p_{g_{\theta^\prime}}(x)$近似，故帶入式子

$$
\mathbb{E}_{p_{g_{\theta}}(x)}\left[ \log (D(x)) \right] + KL(p_{g_{\theta}}(x) || p_{g_{\theta^\prime}}(x))
$$

生成器除了要去騙過判別器外，我們還要求生成器要跟過去的自己接近，意思就是不要更新太快，這個跟一些訓練GAN常用的技巧是相同的，例如gradient penalty，在蘇大神的文章中有做實驗，真的會幫助GAN的訓練與結果

結語

這篇花了不少時間讀懂參考資料，用自己的理解再重新詮釋過，能用一致的角度來看這兩個模型，還是很有收穫的，也更能看清楚模型根本優劣，下一篇還沒想到要寫什麼，敬請期待！

Refernece

• 用变分推断统一理解生成模型（VAE、GAN、AAE、ALI）By 苏剑林
• Lecture #17 (Eric): Deep generative models (part 1): Overview of the theoretical basis and connections of deep generative models
• On Unifying Deep Generative Models

今年在 PyconTW 給的演講，主題是關於機率程式語言與Pyro，機器學習核心問題其中之一是如何建立機率模型，我們想要足夠複雜但又可以推論、訓練的模型，且方法要夠通用兼顧效率；如果有一個生成模型，我們能不斷的從模型抽樣產生樣本，我們就會知道說模型的哪些「設定或是輸入」會產出好的或是跟真實資料相似的樣本，我們可以透過抽樣來推估給定真實資料下，一些隱藏變量或是我們想估計的變數

用機率程式語言來描述一個生成模型或是資料產生的過程，我們可以很容易得去抽樣或是計算機率值，甚至不用去寫複雜的推論過程，機率語言很自然的提供了相對應的推論方法，這些設計都是嵌入在程式語言的設計中

機率程式語言除了建立生成模型，本質上它還是一個通用的程式語言，我們依然可以用它來寫各種複雜程式，例如下西洋棋或是影像渲染等等，這大幅擴展了生成模型所能定義的事，我們不只能去生成影像、語音等等資料，更可以去生成一連串的動作、或是經過渲染的影像，但這些因為都是用機率程式語言所寫的，完全都可以去推估程式中的變量，模型也當然能夠生成新的資料用於預測；認知科學家研究人類如何做決策的過程，常用機率程式語言去假設人類做決策的生成模型，並且給一些人類決策過程的資料，透過這樣來研究所假設的模型是否合理，除此之外，模型在輸出每次的決策同時都可以給出相對應的機率值，與程式內部的變量值，我們可以知道模型為何做這樣的決策，或是如何犯錯的

近年來結合深度學習與自動微分工具，有不少機率程式語言的研究相繼提出，雖然還尚未有殺手級的應用，但是我想這個領域一定會提供人工智慧領域發展很多的新觀點

之前漫談了 Variational Inference ，基本上從機器學習與機率分佈近似的角度出發來談了理論與應用，我們旨在最小化ELBO，來最大化對於資料的解釋，而且從中學習到隱變量，且隱變量還能捕捉到資料潛在資訊，這樣的演算法非常精緻優雅，是我個人非常欣賞的模型；我們的大腦，或是更廣泛來說，一個需要與環境交互的生物或自組織系統，隨時都在對抗失序(resisting a tendency to disorder)，生命需要維持一定的秩序才能生存，各種生理運作都必須精準穩定維持某種秩序，簡言之，維持穩定是生存的要務之一。

對於大腦來說，所謂的穩定就是對於各種輸入大腦都能給予解釋，大腦討厭surprise！大腦討厭無法解釋的東西，或是與自己預期差異很大的狀況，所以大腦的任務就是解釋或是預測各種輸入，來減少遇到surprise，這個概念為 The free energy principle。

The free energy principle 跟 Variational Inference 非常有關係，核心數學概念是相同的，由Karl Friston於2005提出，2010年於Nature上有一篇完整的概念描述 The free-energy principle:a unified brain theory ?，本篇會基於此文章來跟大家介紹這個概念；另外，2017年 Rafal Bogacz 寫了一篇 A tutorial on the free-energy framework for modelling perception and learning，這篇帶領讀者入門一些計算細節，本系列會基於這兩篇文章內容與大家分享。

The free energy principle

• 外部狀態(External states)：會依agent產生的action與隱變量$\vartheta$改變，同時受到隨機干擾$\tilde {w}$的影響
• 感知(Sensation)：觀測外部狀態$\tilde{x}$與隱變量$\vartheta$得到感知$\tilde{s}$
• 內部狀態(Internal states)：最小化Free energy得到最佳的解釋$\mu$
• 決策行為：最小化Free energy來得到最佳的行為$a$

整個流程是一個動態的過程，每個變數都有初始值，透過這樣的循環，agent可以最大化對於環境狀態的了解，內部狀態$\mu$一開始可能完全是隨機的，但透過感知與行為來最小化Free energy，最後內部狀態會從外部狀態中獲取最多資訊

Free energy

其實Free energy就是我們之前提到過的ELBO，差異在於負號，我們希望最小化Free energy，而要最大化ELBO，不過其實從優化角度來看其實一樣

回顧一下ELBO，並且寫成另一個形式
$$
\begin{split}
\mathbb{E}_{q_{\phi}(z)}
\left[
\log \frac{p_{\theta}(x,z)} {q_{\phi}(z)}\right] &= \mathbb{E}\left[ \log p_{\theta}(x|z) \right] - KL(q_{\phi}(z) || p(z)) \\
&= \mathbb{E}\left[ \log p_{\theta}(x,z) \right] - \mathbb{H}\left[ q_{\phi}(z) \right]
\end{split}
$$

上述是以ELBO的角度，需要最大化ELBO，換到Free energy就加上負號，得到下圖的公式，接下來的描述也是以圖上的符號來說明：

Free-energy bound on suprise

• $q(\vartheta | \mu)$ 係指給定內部狀態解釋$\mu$對環境隱變量$\vartheta$的條件機率，跟VI想法一樣，我們無法精確知道隱變量的分佈，只好用一個近似的分佈來估計，所以我們如果對環境有好的解釋，我們應該可以把隱變量估計得比較好
• $p(\tilde { s } , \vartheta|m)$ 給定目前模型$m$，生成$\tilde{s},\vartheta$聯合機率分佈
• 可以對照上述ELBO式子，是完全對應的，整個Free energy 可以寫成 $F ( \tilde { s } , \mu )$，我們可以分別針對兩個變量來最小化

Perception optimizes predictions

• $\mu = \arg \min F ( \tilde { s } , \mu )$
• 根據現在輸入的感知，調整內部狀態$\mu$來最小化$F$，這個跟VI做的事情一樣，去學習好的表徵

Action minimizes prediction errors

• $a = \arg \min F ( \tilde { s } , \mu )$
• 這裡就是有趣的地方了，其實除了可以透過改變解釋來減少$F$，agent也可以透過改變輸入的感知來優化，意思是agent會去選擇比較符合期待感知輸入，這個也稱為active inference

Agent長期而言希望能最小化surprise，其實就是在最小化Free energy，透過改變自己對於感知輸入的解釋，透過主動選擇感知輸入來源與行為，讓agent能快速的了解適應環境；Free energy 是很有機會做為大腦學習、控制的基礎理論，在 The free-energy principle:a unified brain theory ? 文中有介紹與其他現有理論的關係，像是 Neural coding、Bayesian brain hypothesis 等等

結語

智慧的本質到底是什麼？我們到底是如何快速的學習？又為何要學習？本篇介紹了The free energy principle，我想我們為了要生存，必須要抵抗失序，我們必須讓自己維持在一種認知穩地的狀態，這樣帶來的附加效益就是讓我們有快速的學習能力，最終我們成了一個強大的解釋與預測機器

下一篇會介紹 A tutorial on the free-energy framework for modelling perception and learning 這篇文章，提出一個神經網路的框架能執行基於Free energy principle的計算，相當有趣！敬請期待

Refernece

• Free energy principle - Wiki
• The free-energy principle: a unified brain theory?
• A tutorial on the free-energy framework for modelling perception and learning
• Karl Friston 15分鐘訪談 - Free Energy Principle
• Karl Friston 演講影片 - Free energy and active inference

本篇是漫談 Variational Inference 系列第二篇，前一篇介紹了隱變量模型並推導出了ELBO，而我們知道只要有辦法最大化ELBO，就可以去近似$\log_{\theta}p(x)$，但具體而言我們該如何計算呢？

今天我們來細談一下Auto-encoding variational Bayes這篇論文，基於最大化ELBO，引入深度神經網路、低變異的梯度訓練方法提出 Variational Autoencoder(VAE)，把VI方法應用推展至複雜真實資料上，並且有大規模訓練的優化方法，是一篇非常重要且值得一讀的論文！

Auto-encoding variational Bayes

Amortized inference

隱變量模型假設下，每個訓練資料中的觀測變量$x^i$，都對應各自隱變量分佈$z^i \sim q_{\phi_i}(z)$，$z^i$我們稱為局部變數，而$\phi_i$為局部變數的參數；但是當有一個不在訓練資料的新觀測變量$x^j$時，我們沒有對應的隱變量$z^j$的分佈呀！而且訓練過程中需要儲存大量的局部變量，訓練資料集中每一個觀測資料都要分配一組參數來訓練，用這種方法大幅限制了隱變量模型的應用範圍

局部變量$(x^i ,z^i \sim q_{\phi_i}(z))$是個瓶頸，我們引入一個神經網路來直接從觀測變量去預測出隱變量$(x^i ,z^i \sim q_{\phi}(z|x))$，這個神經網路通常也稱為Inference network或是Encoder，此時$\phi$不在是局部變數的參數了，對於計算每個隱變量$z$都是用同樣一組$\phi$，所以是變成全局變量參數，再也不用去儲存每個隱變量，而是可以透過觀測變量來預測，就算對於新的資料也一樣，這個技巧稱為Amortized inference

所以我們把ELBO改成
$$
\mathbb{E}_{q_{\phi}(z|x)}\left[ \log p_{\theta}(x|z) \right] - KL(q_{\phi}(z|x) || p(z))
$$

$q_{\phi}(z|x)$把觀測變量轉換至隱變量，而$p_{\theta}(x|z)$則把隱變量轉換回觀測變量，這樣的架構組成為Encoder-Decoder自編碼器架構，故ELBO的第一項其實就是自編碼器的還原誤差，一個觀測變量經過編碼、解碼後要跟輸入盡可能相同

圖片來源：VARIATIONAL INFERENCE & DEEP LEARNING: A NEW SYNTHESIS

Black Box Variational Inference

我們已經得到一個可以求解優化的式子，並且引入神經網路至框架中，最後就要來看看到底要怎麼訓練這個模型，當然拿出最常用的方法隨機梯度下降(SGD)來試看看囉

要用上SGD，要先知道$\theta,\phi$對目標函數的梯度該如何計算，首先來回憶一下目標函數：
$$
L(\phi,\theta) = \mathbb{E}_{q_{\phi}(z|x)}\left[ \log p_{\theta}(x|z) \right] - KL(q_{\phi}(z|x) || p(z))
$$

先來看$\nabla_{\theta}L(\phi,\theta)$長什麼樣子

$$
\nabla_{\theta} L(\phi,\theta)= \mathbb{E}_{q_{\phi}(z|x)}\left[\nabla_{\theta} \log p_{\theta}(x|z) \right]
$$

因為$\theta$只跟$L(\phi,\theta)$的第一項有關係，所以直接對期望內的$\log p_{\theta}(x|z)$取微分，而第二項無關$\theta$直接為0

再來看$\nabla_{\phi}L(\phi,\theta)$，$\phi$同時跟兩個項都有關係，但仔細看第二項，當$q_{\phi}(z|x)$與$p(z)$都是高斯分佈時，其KL距離可以有公式解，故其對$\phi$的微分也有公式解，所以只有第一項是需要使用抽樣來近似梯度

$
\begin{split}
\nabla_{\phi}L(\phi,\theta) &= \nabla_{\phi} \mathbb{E}_{q_{\phi}(z|x)}\left[\log p_{\theta}(x|z) \right] + \nabla_{\phi}KL(\dots)\\
&\approx \nabla_{\phi} \int q_{\phi}(z|x) \log p_{\theta}(x|z) dz \\
&\approx \int \nabla_{\phi}q_{\phi}(z|x) \log p_{\theta}(x|z) dz \\
&\approx \int q_{\phi}(z|x)\nabla_{\phi}\log q_{\phi}(z|x) \log p(x|z) dz \\
&\approx n \log p_{\theta}(x|z)\nabla_{\phi}\log q_{\phi}(z|x) \quad z \sim q_{\phi}(z|x)
\end{split}
$

推導過程中用上了一個技巧，稱為log-derivative trick

$$
\nabla_{\phi}\log q_{\phi}(z|x) = \frac{\nabla_{\phi}q_{\phi}(z|x)}{q_{\phi}(z|x)}
$$

所以可以把$\nabla_{\phi}q_{\phi}(z|x)$代換掉，得到一個能用抽樣近似的式子。所以總結一下上述的推導，$\nabla_{\theta}L(\phi,\theta)$是在訓練我們的生成模型，也可以說是Decoder，最大化$p_{\theta}(x)=p_{\theta}(x|z)p(z)$，這裡等同於EM演算法中的M步驟；而$\nabla_{\phi}L(\phi,\theta)$含有兩個部分，一個部分是KL的微分項，有解析公式容易計算，但另一項的積分就只能靠抽樣來近似，抽樣出$z$並計算對$\phi$梯度與資料似然加總，得到沒有偏差(Unbiased)的梯度估計

Reparametrization-based low-variance gradient estimator

上一小節我們得到了參數對於目標函數的梯度，但還有個問題，就是$\nabla_{\phi}L(\phi,\theta)$的變異(variance)非常的大，$n \log p_{\theta}(x|z)$有可能會是非常大的值而使得梯度過大；梯度是向量來描述要往哪邊走，才會使得目標函數最小，當變異很大時，就像是每個人都說要往不同的方向走，到最後這些方向加總在一起反而依然在原地打轉，或是有一個人說要往某個方向走非常大的一步，大過於其他人而造成梯度是有偏誤的，雖然期望上$\nabla_{\phi}L(\phi,\theta)$是個不偏估計，但是梯度變異過大使得訓練參數很困難

本篇論文的另一個重點就是用上Reparametrization trick於梯度估計上，提出一個低變異的梯度估計方法，才使得VAE能穩定訓練；我們將隨機的抽樣過程 $z \sim q_{\phi}(z|x)$，改成一個決定性的計算過程，例如要從高斯分佈中抽樣，我們可以改成

$$
z = g_{\mu, \sigma}(\epsilon) = \mu + \epsilon \cdot \sigma, \quad \epsilon \sim N(0,1)
$$

圖片來源：VARIATIONAL INFERENCE & DEEP LEARNING: A NEW SYNTHESIS

抽樣會使得梯度無法傳遞，就像左邊那張圖一樣，Z是一個隨機計算節點，經過Z後我們無法對之前的計算有任何資訊，自然也無法計算梯度，但改成Reparameterized form後，梯度就能順利回傳至參數上；另一點是有效減少梯度變異，原本梯度計算過程受$n \log p_{\theta}(x|z)$影響而造成變異過大，而現在我們只需要計算$\nabla_\phi f$的期望值，兩者數值大小差異很大，因此減少梯度變異使訓練過程穩定，才能用在複雜的資料集上

$$
\nabla_\phi \mathbb{E}_{z \sim q(z\mid x)}\left[ f(x,z) \right] = \mathbb{E}_{\epsilon \sim p(\epsilon)} \left[ \nabla _{\phi} f(x,g(\epsilon, x))\right]
$$

結語

本篇是漫談VI方法的第二篇，細談了VAE模型基礎，如何從ELBO對應到自編碼器架構，且$KL(q_{\phi}(z|x)||p(z))$也可以看成是一種正規化項，並提出改進的梯度估計方法，才能使得訓練模型成為可能，VAE是非常好的表徵學習方法，訓練穩定並能結合半監督式學習、增強學習等技術，後續很多的理論改進應用延伸，值得關注與學習

下一篇會討論VAE與其他生成模型的關係，最近有一些工作討論將各種生成模型放入同一個框架內討論，敬請期待

Refernece

• CS228/The variational auto-encoder
• Black Box Variational Inference

序列資料模型我們常用LSTM、或是各種RNN的變形，在主流的各種任務上都取得了非常好的結果，如機器翻譯、序列生成等；但因為遞迴特性，訓練過程很難平行化計算，難以利用硬體加速，此外，RNN模型依然存在記憶遺忘問題，很難捕捉序列的長期關係

近年來出現不少不是基於RNN序列模型，這篇When Recurrent Models Don’t Need to be Recurrent分析兩種模型於序列模型上的差異，非基於RNN模型如之前介紹的Wavenet，是一種Feed-Forward序列生成的模型，本篇要介紹的是Attention Is All You Need，論文名稱很霸氣，果然有實力要叫什麼名字都可以XD，模型完全只使用注意力機制來做序列模型，在機器翻譯任務上，不僅訓練速度快且效果也非常好，很值得來實作的一篇論文；在後續研究上，注意力機制被用在更多的領域上，例如Self-Attention Generative Adversarial Networks，本篇論文也是扮演重要的承先啟後角色

Model Architecture

論文提出模型稱為Transformer，這篇The Illustrated Transformer介紹非常完整，而且還有動畫來說明，強烈建議先看看這篇，本篇文章就稍微偷懶只簡單談一下其中一些細節心得與看法

Scaled Dot-Product Attention

注意力機制可以視為類似搜尋的過程，給一個你想搜尋的Query，Query去跟Key做內積看看相近程度，然後用softmax來正規化來得到注意力分佈，最後根據這個注意力分佈來加權Value得到結果，整個過程公式簡單明瞭，僅是矩陣相乘

Multi-Head Attention

Multi-Head Attention其實也沒什麼，就只是把Q、K、Ｖ分成好幾個部份，然後經過Linear轉換，再將每個部份分別去做Scaled Dot-Product Attention最後黏起來，好處就是讓整個注意力機制過程變得更彈性、可訓練，每個部分可以有不一樣的注意力權重

Encoder & Decoder

Encoder與Decoder都是由Block堆疊而成，Block裡面基本上由上一小節介紹的Multi-Head Attention與Feed Forward組成，但是EncoderBlock僅用到Self attention，意思是Multi-Head Attention中的Q,K,V都是同一個輸入

論文裡給了Encoder中5-6層的Attention結果，可以看到Self attention表示了句子中某一個字與其他字之間的關係，且因為是Multi-Head的關係，圖上有不同顏色區分不同部分；Encoder利用Self attention來提取整個序列的結構，且沒有沒有遺忘問題，序列上每個位置都與其他位置考慮到之間關係，計算也相當快速

Decoder在進行解碼時，也先做Self attention來把目標序列的結構考慮進來，然後再引入Encoder的訊息做Multi-Head Attention，最後預測出序列下一個位置

Implement and Tricks

我的實作版本，以pytorch實作並於IWSLT16英文-德語翻譯語料進行訓練與測試

Data preprocessing

把原始資料變成可以訓練的Dataloader常常要花一番苦工，Pytorch提供一系列不同的工具，像是torchvision、torchaudio、torchtext，裡面有一些整理好的資料集或是常用函數，不論是要自己重新做一個新資料集或是直接使用都非常方便，而且減少錯誤機會，所以基本上我不太喜歡自己去重寫資料整理的部分，而是去學習使用已有且穩定的套件

torchtext其實是有直接提供IWSLT16 dataloader使用，但是有些錯誤，所以沒辦法順利直接利用，那只好利用所提供的函數自己來做一個囉

要做一個翻譯的資料集相當簡單，只需要把語料資料整理成兩個文件(也可以是多個，用檔名區分即可)分別對應，像是這樣：

1
2
3
4
5
6

#train.de.txt

David Gallo: Das ist Bill Lange. Ich bin Dave Gallo.
Wir werden Ihnen einige Geschichten über das Meer in Videoform erzählen.
Wir haben ein paar der unglaublichsten Aufnahmen der Titanic, die man je gesehen hat,, und wir werden Ihnen nichts davon zeigen.
...

1
2
3
4
5
6

#train.en.txt

David Gallo: This is Bill Lange. I'm Dave Gallo.
And we're going to tell you some stories from the sea here in video.
We've got some of the most incredible video of Titanic that's ever been seen, and we're not going to show you any of it.
...

用spacy來做斷詞，並告訴torchtext.data.Field所使用的斷詞器、與相關參數設定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

spacy_de = spacy.load('de')
spacy_en = spacy.load('en')


def tokenize_en(text):
    return [tok.text for tok in spacy_en.tokenizer(text)]
def tokenize_de(text):
    return [tok.text for tok in spacy_de.tokenizer(text)]

DE = data.Field(tokenize=tokenize_de,
                init_token='<SOS>',
                eos_token='<EOS>',
                fix_length=20,
                lower=True,
                batch_first=True)
EN = data.Field(tokenize=tokenize_en,
                init_token='<SOS>',
                eos_token='<EOS>',
                lower=True,
                fix_length=20,
                batch_first=True)

用torchtext.datasets.TranslationDataset把語料包裝成datasets

1
2
3

train = datasets.TranslationDataset(path='./data/train', 
                                    exts=('.de.txt', '.en.txt'),
                                    fields=(DE, EN))

還有製作字典

1
2

DE.build_vocab(train.src, min_freq=3)
EN.build_vocab(train, max_size=50000)

最後就可以包裝成Dataloader了

1
2
3
4
5
6
7
8

train_iter = data.BucketIterator(dataset=train, 
                                 batch_size=32,
                                 sort_key=lambda x: data.interleave_keys(len(x.src), len(x.trg)))
                                 
train_batch = next(iter(train_iter))
train_batch[0].src
> tensor([[   2,    6,  195,  437,   13,   82, 2076,    0,    5,    3,    1,    1,
            1,    1,    1,    1,    1,    1,    1,    1]], device='cuda:0')

以上很簡單介紹用法，這裡還有兩篇(1,2)不錯的教學，大家可以參考

Mask is important

Transformer模型不難理解與實作，但是有個小地方尤其重要，就是輸入需要很仔細地做Mask，非Recurrent模型有個問題，就是輸入長度、大小都必須要是固定的，不管句子長短，要輸入至模型都需要截長補短至固定長度，所以當句子短時候，後面會補上PAD來填滿長度，但是些部分是不能參與至注意力過程的，所以我們每次去做矩陣相成後，需要把某些部分遮起來

1
2
3
4
5
6
7

output = torch.bmm(Q,K.transpose(1,2))
output = output / ( self.hidden_size**0.5)

queries_mask_ = torch.cat([queries_mask]*self.num_head,0).float()
keys_mask_ = torch.cat([keys_mask]*self.num_head,0).float()
output_mask = 1 - queries_mask_.bmm(keys_mask_.transpose(1,2)).float()
output_ = output.masked_fill(output_mask.byte() , -2**32)

這部分可以配合實作一起看會比較清楚，queries_mask_與keys_mask_是輸入時候給的，告訴模型這個序列的長度資訊，是PAD地方為0其餘為1

既然output是Q,K相乘，我們如果把他們的mask也相乘，就可以得到正確的mask，mask為0的地方代表是PAD去做注意力過程，應該要被忽略

最後用masked_fill來把要忽略的位置填上一個很小的數值，因為masked_fill是把為1的地方填上，所以之前算出來的mask要做反轉，至於為何要填上很小的負數值是因為等一下要做softmax，如果單純填上0，經過softmax可能不為0

Causality is important

Decoder在解碼的時候是基於過去的序列來預測下一個位置，當然不能看到未來的訊息，所以Decoder裡做Self attention要把未來資訊遮蔽，實作上很簡單就是做一個上三角矩陣，但是要保留對角線部分

1
2
3
4
5
6

if self.causality:
    bs,s1,s2 = output_mask.size()
    tri = np.triu(np.ones((s1,s2))) - np.eye(s1,s2)
    tri = torch.from_numpy(tri).to(output_mask.device)
    tri = torch.stack([tri]*bs,0).byte()
    output_ = output_.masked_fill(tri , -2**32)

這樣就能保證Decoder訓練過程不會去偷看到下一個位置，只能用自己現在與過去的位置資訊來預測

Reference

• Attention Is All You Need
• The Illustrated Transformer
• The Annotated Transformer
• Kyubyong/transformer
• jadore801120/attention-is-all-you-need-pytorch

Variational Inference 是一種近似複雜分佈的數學方法，我們假設一類計算簡單的候選分佈$q(z)$，並有另一個複雜難以計算的後驗分佈$p(z|x)$，我們希望從候選分佈中找一個最接近$p(z|x)$的$q^*(z)$，這個等同於最小化$KL(q(z) | p(z|x))$

不過為什麼我們要近似後驗分佈$p(z|x)$呢？或是$q(z)$可以怎麼定義？與深度學習怎麼結合？本篇或接下來的幾篇文章就來跟大家漫談一下VI，整理了自己看過有關的資料，從幾個角度切入推導，並來看看跟其他生成模型有什麼關係

Latent variable model

要談VI之前要先講一下隱變量模型(Latent variable model)，因為VI就是拿來求解隱變量模型方法之一，我們假設可觀測的隨機變數$x$與無法觀測的隱變量$z$聯合機率分佈為：

$$
p_{\theta}(x,z) = p_{\theta}(x|z)p(z)
$$

其中$p_{\theta}(x|z)$為一個參數化的模型來表示條件機率，再透過把$z$積分，我們可以得到$p(x)$：

$$
p_{\theta}(x) = \int p_{\theta}(x,z)dz
$$

看來很完美，我們得到$p(x)$式子接著就能直接去用MLE去學習 $\theta$ 囉！

這裡再多討論一下為何要使用隱變量模型，從上面式子來看，引入隱變量可以幫助我們定義出一個能計算的$p(x)$，解決了不知道怎麼假設$p(x)$的問題；另外，隱變量能捕捉資料所隱含的特性，例如「星座」是人們所加上的隱變量，有時候透過「星座」可以更快掌握你是個怎樣的人或是個性，或是說從你的行為來猜測你是什麼星座之類的，都是生活中常見的隱變量應用

不過更多時候，隱變量於表徵學習任務上扮演重要的角色，像是這個手繪塗鴉的例子，所學習到的隱變量於低維度可以形成流型(Manifolds)，隱變量能捕捉資料的變異性，形成一個漸變的空間且具有泛化能力，代表隱變量能更好的表示資料特性，是很好的表徵學習方法

計算後驗機率困難

我們先來看看為什麼要近似$p(z|x)$，從隱變量模型，我們有一個可以計算的$p(x,z)$，現在把$p(x)$重新寫成：

$$
p(x) = \frac{p(x,z)}{p(z|x)}
$$

又是另一片天地，我們想要能計算$p(x)$，那只要$p(x,z)$與$p(z|x)$都可以被計算，那一切就太好了；只可惜，$p(z|x)$是無法被計算的，原因是：

$$
p(z|x) = \frac{p(x,z)}{p(x)}
$$

又導回來了，我們就是苦於沒有$p(x)$呀，那只好直接用另一個$q(z)$來偽裝成$p(z|x)$了，如果他們兩個夠相似，$p(x)$應該是可以被近似求出來的，這裡就用上VI想法了！

Evidence Lower Bound

我們希望用上$q_{\phi}(z)$來取代$p_{\theta}(z|x)$解決後驗計算困難問題，所以引入$q_{\phi}(z)$至$p(x)$得到：

$
\begin{split}
\log p_{\theta}(x) &= \mathbb{E}_{q_{\phi}(z)} \left[ \log p_{\theta}(x) \right] \\
&= \mathbb{E}_{q_{\phi}(z)} \left[ \log \frac{p_{\theta}(x,z)}{p_{\theta}(z|x)} \right] \\
&= \mathbb{E}_{q_{\phi}(z)}
\left[
\log \frac{p_{\theta}(x,z)}{q_{\phi}(z)} \frac{q_{\phi}(z)}{p_{\theta}(z|x)}
\right] \\
&= \mathbb{E}_{q_{\phi}(z)}
\left[
\log \frac{p_{\theta}(x,z)}{q_{\phi}(z)}\right] + \mathbb{E}_{q_{\phi}(z)} \left[ \log \frac{q_{\phi}(z)}{p_{\theta}(z|x)}
\right] \\
&= \mathbb{E}_{q_{\phi}(z)}
\left[
\log \frac{p_{\theta}(x,z)} {q_{\phi}(z)}\right] + KL(q_{\phi}(z)|| p_{\theta}(z|x))
\end{split}$

我們將原本$\log_{\theta} p(x)$拆成兩項，先來看第二項，為我們VI方法裡面的候選分佈$q_{\phi}(z)$與後驗分佈$p_{\theta}(z|x)$的KL距離，一定大於等於0，但我們依然無法直接去最小化之間差距

所以轉看第一項，又因$\log p(x)$為一個定值，第一項就成為了一個下界(Lower Bound)並稱為Evidence Lower Bound(ELBO)，如果我們最大化第一項，不就等同於最小化第二項了嗎！而且第一項完全是可以算的！我們能透過訓練參數$\theta , \phi$來最大化ELBO，同時也減少$q_{\phi}(z)$與$p_{\theta}(z|x)$KL距離

最後整理成一般常看到ELBO形式

$$
\mathbb{E}_{q_{\phi}(z)}
\left[
\log \frac{p_{\theta}(x,z)} {q_{\phi}(z)}\right] = \mathbb{E}\left[ \log p_{\theta}(x|z) \right] - KL(q_{\phi}(z) || p(z))
$$

Importance Sampling to ELBO

剛剛我們由計算後驗分佈困難而推導出了ELBO，這次我們從 Importance Sampling 出發來推出ELBO，計算$p_{\theta}(x)$是求解一個複雜的積分：
$$
p_{\theta}(x) = \int p_{\theta}(x|z)p(z)dz
$$

我們可以用 Importance Sampling 來近似這個積分，用一個簡單的$q_{\phi}(z)$來抽樣出$z$，並且根據$\frac{q_{\phi}(z)}{p(z)}$來決定抽樣出的樣本權重：

$
\begin{split}
p_{\theta}(x) &= \int p_{\theta}(x|z) \frac{p(z)}{q_{\phi}(z)} q_{\phi}(z)dz \\
&= \int p_{\theta}(x|z)w^{(s)}q_{\phi}(z)dz \quad w^{(s)} = \frac{p(z)}{q_{\phi}(z)} \\
&\approx \frac{1}{S} \sum w^{(s)}p(x|z^{(s)})
\end{split}$

這裡用上Jensen’s inequality：

$$
\log \int p(x)g(x) dx \ge \int p(x) \log g(x) dx
$$

代入得到：

$
\begin{split}
\log p_{\theta}(x) &= log \int p_{\theta}(x|z) \frac{p(z)}{q_{\phi}(z)} q(z) dz \\
&\ge \int q_{\phi}(z) \log \left[ p_{\theta}(x|z)\frac{p(z)}{q_{\phi}(z)} \right] dz = \int q_{\phi}(z) \log_{\theta}(x|z) - \int q_{\phi}(z) \log \frac{q_{\phi}(z)}{p(z)} \\
\end{split}$

最後將式子整理成：

$$
\int q_{\phi}(z) \log_{\theta}(x|z) - \int q_{\phi}(z) \log \frac{q_{\phi}(z)}{p(z)} = \mathbb{E}\left[ \log p_{\theta}(x|z) \right] - KL(q_{\phi}(z) || p(z))
$$

Variational EM

最後我們來給一個具體常用來求解隱變量模型的演算法，最大期望演算法(Expectation-Maximization Algorithm,EM)，這裡不打算從頭講起EM，但是這個演算法相當重要，值得深入了解，我推薦最近剛結束的DeepBayes課程，裡面非常詳細介紹了EM方法，本小節也有參考課程資料

用EM求解高斯混和模型(Gaussian Mixed Model)時候，因為高斯分佈良好的性質，所以能很方便地得到公式解：

• E-step：$q(z) = p(z|x,\theta)$
• Ｍ-step：$\max\limits_{\theta} \mathbb{E}\left[ \log p_{\theta}(x,z) - \log q(z) \right]$

可以看到在E-step時候，$q(z)$總是有公式解，故我們是有一個最優的$q(z)$恰好等於$p(z|x)$，也就等於最小化$KL(q(z)|p(z|x))$為0，M-step訓練參數$\theta$來最大化$\log p_{\theta}(x)$，此時ELBO直接等於$\log p_{\theta}(x)$

但很多時候我們無法寫出E-step的公式解，所以我們就用上VI方法，並且假設候選分佈為一個簡單且每個分量皆為獨立的分佈$q(z)=\prod q(z_i)$，稱為Mean-Field Approximation，我們帶入回ELBO中可以得到

$
\begin{split}
ELBO(q, \theta) & = \int \prod_i q_i(z_i) \Big[ \log p_{\theta}(x,z) - \sum_i \log q_i(z_i) \Big ]dz \\
& = \int q_j(z_j) \Big [ \int \log p_{\theta}(x,z) \prod_{i \neq j} q_i(z_i)dz_i \Big ] dz_j - \int \sum_{i \neq j} \log q_i(z_i) \prod_{i \neq j} q_i(z_i)dz_i - \int q_i(z_i) \log q_i(z_i)dz_i \\
& = \int q_j(z_j) \log \tilde p(x,z_j)dz_j - \int q_j(z_j) \log q_j(z_j) dz_j + const \\
& = -KL(q_j(z_j) || \tilde p(x,z_j))
\end{split}
$

最後 Variational EM 我們可以寫成

• E-step：$q_j(z_j) \propto \tilde p(x,z_j)$
• Ｍ-step：$\max\limits_{\theta} \mathbb{E}\left[ \log p_{\theta}(x,z) - \log q(z) \right]$

計算$q_j(z_j) = \mathbb{E}_{i \neq j}\left[ \log p(x,z) \right]$，固定$z_j$然後將j以外的維度進行積分，白話一點就是固定一個維度，把其他維度的所有組合都試過一次來計算這個維度的機率分佈，涉及非常大量的計算，雖然Mean-Field Approximation一定能寫成這樣的解，但是很多時候依然無法計算

結語

本篇是漫談VI方法的第一篇，介紹了隱變量模型與其求解困難，並用上VI方法來求解模型，得出可以透過最大化ELBO來求解訓練參數，最後介紹了Variational EM方法與限制

第一篇算是基礎介紹，也是我論文裡文獻回顧又再回顧一次，介紹了兩種角度推導出ELBO，下一篇我打算來介紹與深度學習如何結合，突破Mean-Field Approximation限制，成為生成模型中一個重要的方法，敬請期待

Reference

• NIPS 2016 Tutorial，很完整介紹VI的發展歷史 Variational Inference: Foundations and Modern Methods
• Shakir Mohamed 大神的教學投影片Variational Inference for Machine Learning
• VAE 提出者的博士論文，值得一看！VARIATIONAL INFERENCE & DEEP LEARNING: A NEW SYNTHESIS
• Expectation Maximization and Variational Inference