沒想到一晃眼就是一年了,但自己挖的坑還是要填完,希望又能開始恢復寫部落格的習慣,也把自己關注的研究陸續整理上來,期待能獲得一些新想法,要訓練自己能用多個角度去看同一個問題,能把多個問題歸納成同一個框架
本篇是漫談 Variational Inference 系列第三篇,第二篇介紹了VAE,把深度學習與VI做個結合,也引領出了很多後續的研究;而本篇來談談VI方法跟一些其他生成模型的關係,用一致的框架來討論VAE與GAN
New formulation of VAE
首先我們有 $q_{\phi}(x,z)=q_{\phi}(z|x)p(x)$ 與 $p_{\theta}(x,z)=p_{\theta}(x|z)p(z)$,那來對上一篇VAE的ELBO計算期望值
$
\begin{split}
E_x \left[
E_{q_{\phi}(z|x)}
\left[ \log \frac{p_{\theta}(x,z)} {q_{\phi}(z|x)}\right]
\right] &= E_{q_{\phi}(x,z)}
\left[ \log \frac{p_{\theta}(x,z)} {q_{\phi}(z|x)}\right] \\
&= E_{q_{\phi}(x,z)}
\left[ \log \frac{p_{\theta}(x,z)} {q_{\phi}(z|x)} + \log p(x) - \log p(x) \right] \\
&= E_{q_{\phi}(x,z)}
\left[ \log \frac{p_{\theta}(x,z)} {q_{\phi}(x,z)} + \log p(x) \right] \\
&= KL(q_{\phi}(x,z) || p_{\theta}(x,z)) + C
\end{split}
$
做了一些變換後,可以把ELBO表示成兩個聯合機率分布的KL距離,我們關注的是 $p_{\theta}(x,z)$,希望可以生成很真實的樣本,KL是個非對稱的divergence,交換位置是完全不同的效果,生成器$p_{\theta}(x,z)$於計算KL的位置會影響優化的目標,這也導致了VAE生成樣本比較模糊,但不容易Mode collapse的原因,我們接著來看GAN的形式如何,再來一起討論其異同
New formulation of GAN
接著我們也是看看把GAN整理成類似的形式,方便後續的分析比較,$y$代表真實資料(y=1)或是生成樣本(y=0),現在我們換個角度來看,把$x$當作隱變量而$y$視為可觀測的輸入,我們想用一個候選分佈$p_{\theta}(x|y)$,希望去優化$q_{\phi}(y|x)$這個條件機率(判別器),GAN訓練過程我們會輸入真實資料與生成樣本給判別器去,我們現在的候選分佈應該是由$g_{\theta}(x)$生成與$p_{\text data}(x)$混合而成,所以把$p_{\theta}(x|y)$寫成:
$$
p_{\theta}(x | y)=\left \{
\begin{array}{ll}
{p_{g_{\theta}}(x)} & {y=0} \\
{p_{\text {data}}(x)} & {y=1}
\end{array}\right.
$$
優化的目標也會依訓練過程不同,兩個階段是相反的,候選分佈會隨機給真實資料或是生成樣本,訓練$q_{\phi}(y|x)$判別器分類正確
$$
\max_{\boldsymbol{\phi}} L_{\phi} = \mathbb{E}_{p_{\theta}(\boldsymbol{x} | y)p(y)}\left[\log q_{\phi}(y | \boldsymbol{x})\right]
$$
於訓練$g_{\theta}(x)$生成器階段,我們希望$q_{\phi}(y|x)$分類錯誤,$q_{\phi}^r(y|x)$表示相反的$y$,優化目標變成
$$
\max_{\boldsymbol{\theta}} \mathcal{L}_{\theta}=\mathbb{E}_{p_{\theta}(\boldsymbol{x} | y) p(y)}\left[\log q_{\phi}^r(y | \boldsymbol{x})\right]
$$
跟VAE不同,兩個階段優化的目標並不一樣,這也導致訓練更為困難,我們對訓練生成器階段做個推導整理,並且加上負號來改成最小化
$
\begin{split}
E_{p(y)}\left[
E_{p_{\theta}(x|y)}
\left[ - \log q_{\phi}^r(y | x)\right]
\right] &= E_{p(y)p_{\theta}(x|y)}\left[ \log \frac{q_{\phi}^r(y | x)p_{\theta^\prime}(x)}{p_{\theta}(x|y)p(y)} - \log \frac{p_{\theta}(x|y)p(y)}{p_{\theta^\prime}(x)} \right] \\
&= KL(p_{\theta}(x,y) || q_{\phi}^r(x,y)) - KL(p_{\theta}(x,y) || p_{\theta^\prime}(x))
\end{split}
$
推導過程中我們加入$x$的先驗分佈$p_{\theta^\prime}(x)= \sum_y p_{\theta^\prime}(y|x)p(y)$,訓練生成器時候,我們會由上一輪訓練出來的$g_{\theta^\prime}$生成樣本與真實資料去訓練新的$g_{\theta}$,所以每次先驗分佈都在改變,最後我們得到一個跟VAE類似的結果,但是$p_{\theta}(x,y)$在KL中的位置是相反的
Compare VAE and GAN
Mode covering and collapse
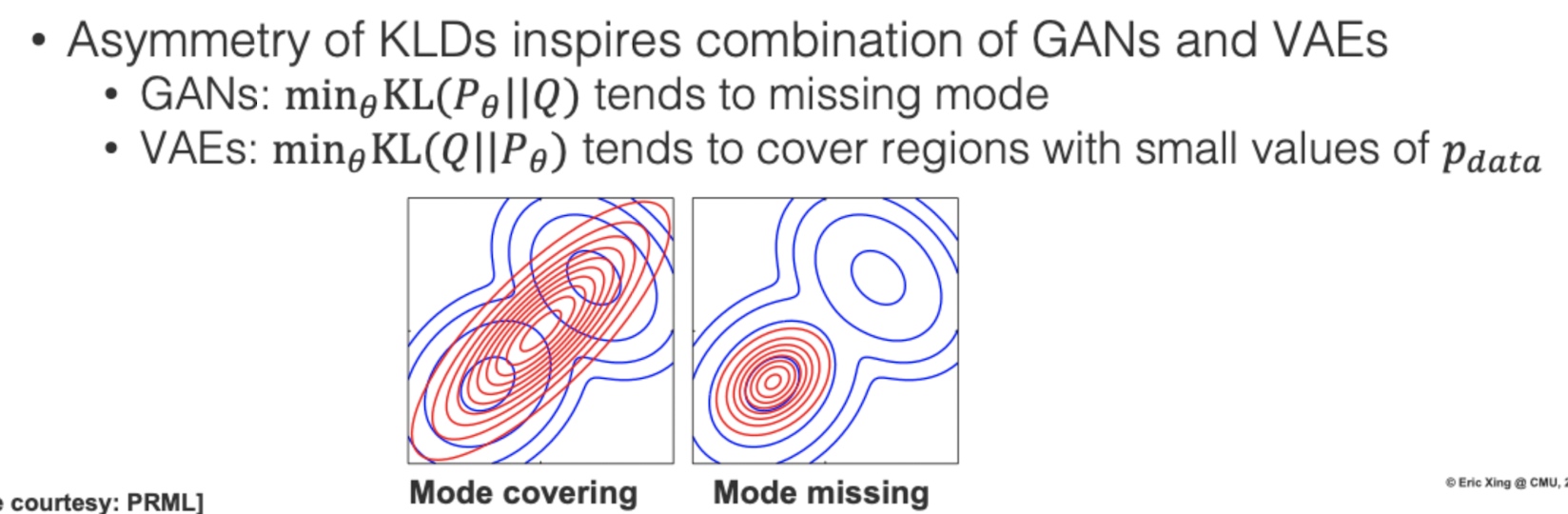
我們看到兩種模型的優化目標是相反的KL divergence,VAE傾向去覆蓋整個分佈,但也可能會覆蓋到一些機率密度低的位置,而使得有時候抽樣出來的影像不夠真實,所以VAE除了使用L2 loss去計算影像還原損失,本身就會導致模糊外,更深一層本質上是KL的特性所導致
GAN則為相反,傾向去學好一個Mode,認真顧好一個部分就好,所以能產生非常真實的資料,但會有Mode collapse
Different prior
推導過程中我們都有引入$x$的先驗分佈,
- VAE:$p(x)$代表的是真實資料分布
- GAN:$p_{\theta^\prime}(x)$代表的是混和分佈
Mixed prior
我們換從訓練判別器階段來分析,我們嘗試把$p_{\theta^\prime}(x)$當作先驗分佈引入在拆解$q_{\phi}(x,y)$時
$
\begin{split}
KL(p_{\theta}(x,y) || q_{\phi}(x,y))
&= \int p_{data}(x) \log \frac{p_{data}(x)}{q_{\phi}(x,y=1)} + \int p_{g_{\theta}}(x) \log \frac{p_{g_{\theta}}(x)}{q_{\phi}(x,y=0)} \\
&= \int p_{data}(x) \log \frac{p_{data}(x)}{q_{\phi}(y=1|x)p_{data}(x)} + \int p_{g_{\theta}}(x) \log \frac{p_{g_{\theta}}(x)}{q_{\phi}(y=0|x)p_{g_{\theta}}(x)} \\
&= \int p_{data}(x) \log \frac{1}{q_{\phi}(y=1|x)} + \int p_{g_{\theta}}(x) \log \frac{1}{q_{\phi}(y=0|x)} \\
&= E_{p_{data}(x)}\left[ \log D(x) \right] + E_{p_{g_{\theta}}(x)}\left[ \log (1-D(x)) \right]
\end{split}
$
我們得到跟原始GAN paper上熟悉的式子!
Data prior
用变分推断统一理解生成模型(VAE、GAN、AAE、ALI)By 苏剑林文章中引入了$p(x)$當作先驗分佈,一開始不太理解文章與原始GAN的關係,後來經過一番梳理,發現原來只是先驗分佈的不同
$
\begin{split}
KL(p_{\theta}(x,y) || q_{\phi}(x,y))
&= \int p_{data}(x) \log \frac{p_{data}(x)}{q_{\phi}(x,y=1)} + \int p_{g_{\theta}}(x) \log \frac{p_{g_{\theta}}(x)}{q_{\phi}(x,y=0)} \\
&= \int p_{data}(x) \log \frac{p_{data}(x)}{q_{\phi}(y=1|x)p_{data}(x)} + \int p_{g_{\theta}}(x) \log \frac{p_{g_{\theta}}(x)}{q_{\phi}(y=0|x)p_{data}(x)} \\
&= \int p_{data}(x) \log \frac{1}{q_{\phi}(y=1|x)} + \int p_{g_{\theta}}(x) \log \frac{1}{q_{\phi}(y=0|x)} + \int p_{g_{\theta}}(x) \log \frac{p_{g_{\theta}}(x)}{p_{data}(x)} \\
&= E_{p_{data}(x)}\left[ \log D(x) \right] + E_{p_{g_{\theta}}(x)}\left[ \log (1-D(x)) \right] + KL(p_{g_{\theta}}(x) || p_{data}(x))
\end{split}
$
實務上,我們訓練生成器都只去優化第二項,引入Data prior後,整個優化項變成
$$
\mathbb{E}_{p_{g_{\theta}}(x)}\left[ \log (D(x)) \right] + KL(p_{g_{\theta}}(x) || p_{data}(x))
$$
我們假設$p_{data}(x)$可以由上一輪的$p_{g_{\theta^\prime}}(x)$近似,故帶入式子
$$
\mathbb{E}_{p_{g_{\theta}}(x)}\left[ \log (D(x)) \right] + KL(p_{g_{\theta}}(x) || p_{g_{\theta^\prime}}(x))
$$
生成器除了要去騙過判別器外,我們還要求生成器要跟過去的自己接近,意思就是不要更新太快,這個跟一些訓練GAN常用的技巧是相同的,例如gradient penalty,在蘇大神的文章中有做實驗,真的會幫助GAN的訓練與結果
結語
這篇花了不少時間讀懂參考資料,用自己的理解再重新詮釋過,能用一致的角度來看這兩個模型,還是很有收穫的,也更能看清楚模型根本優劣,下一篇還沒想到要寫什麼,敬請期待!