本篇是漫談 Variational Inference 系列第二篇,前一篇介紹了隱變量模型並推導出了ELBO,而我們知道只要有辦法最大化ELBO,就可以去近似$\log_{\theta}p(x)$,但具體而言我們該如何計算呢?
今天我們來細談一下Auto-encoding variational Bayes這篇論文,基於最大化ELBO,引入深度神經網路、低變異的梯度訓練方法提出 Variational Autoencoder(VAE),把VI方法應用推展至複雜真實資料上,並且有大規模訓練的優化方法,是一篇非常重要且值得一讀的論文!
Auto-encoding variational Bayes
Amortized inference
隱變量模型假設下,每個訓練資料中的觀測變量$x^i$,都對應各自隱變量分佈$z^i \sim q_{\phi_i}(z)$,$z^i$我們稱為局部變數,而$\phi_i$為局部變數的參數;但是當有一個不在訓練資料的新觀測變量$x^j$時,我們沒有對應的隱變量$z^j$的分佈呀!而且訓練過程中需要儲存大量的局部變量,訓練資料集中每一個觀測資料都要分配一組參數來訓練,用這種方法大幅限制了隱變量模型的應用範圍
局部變量$(x^i ,z^i \sim q_{\phi_i}(z))$是個瓶頸,我們引入一個神經網路來直接從觀測變量去預測出隱變量$(x^i ,z^i \sim q_{\phi}(z|x))$,這個神經網路通常也稱為Inference network或是Encoder,此時$\phi$不在是局部變數的參數了,對於計算每個隱變量$z$都是用同樣一組$\phi$,所以是變成全局變量參數,再也不用去儲存每個隱變量,而是可以透過觀測變量來預測,就算對於新的資料也一樣,這個技巧稱為Amortized inference
所以我們把ELBO改成
$$
\mathbb{E}_{q_{\phi}(z|x)}\left[ \log p_{\theta}(x|z) \right] - KL(q_{\phi}(z|x) || p(z))
$$
$q_{\phi}(z|x)$把觀測變量轉換至隱變量,而$p_{\theta}(x|z)$則把隱變量轉換回觀測變量,這樣的架構組成為Encoder-Decoder自編碼器架構,故ELBO的第一項其實就是自編碼器的還原誤差,一個觀測變量經過編碼、解碼後要跟輸入盡可能相同
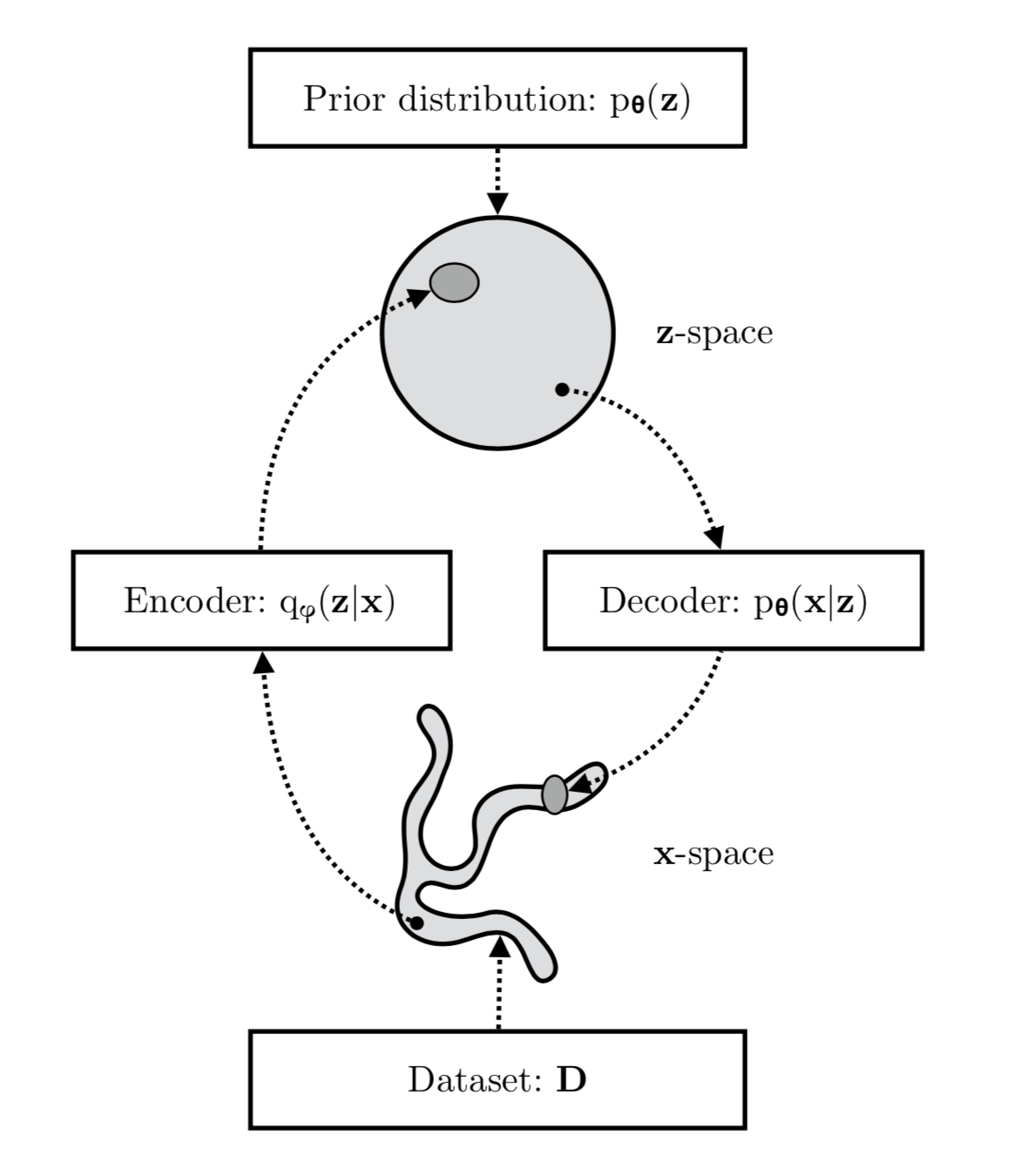
圖片來源:VARIATIONAL INFERENCE & DEEP LEARNING: A NEW SYNTHESIS
Black Box Variational Inference
我們已經得到一個可以求解優化的式子,並且引入神經網路至框架中,最後就要來看看到底要怎麼訓練這個模型,當然拿出最常用的方法隨機梯度下降(SGD)來試看看囉
要用上SGD,要先知道$\theta,\phi$對目標函數的梯度該如何計算,首先來回憶一下目標函數:
$$
L(\phi,\theta) = \mathbb{E}_{q_{\phi}(z|x)}\left[ \log p_{\theta}(x|z) \right] - KL(q_{\phi}(z|x) || p(z))
$$
先來看$\nabla_{\theta}L(\phi,\theta)$長什麼樣子
$$
\nabla_{\theta} L(\phi,\theta)= \mathbb{E}_{q_{\phi}(z|x)}\left[\nabla_{\theta} \log p_{\theta}(x|z) \right]
$$
因為$\theta$只跟$L(\phi,\theta)$的第一項有關係,所以直接對期望內的$\log p_{\theta}(x|z)$取微分,而第二項無關$\theta$直接為0
再來看$\nabla_{\phi}L(\phi,\theta)$,$\phi$同時跟兩個項都有關係,但仔細看第二項,當$q_{\phi}(z|x)$與$p(z)$都是高斯分佈時,其KL距離可以有公式解,故其對$\phi$的微分也有公式解,所以只有第一項是需要使用抽樣來近似梯度
$
\begin{split}
\nabla_{\phi}L(\phi,\theta) &= \nabla_{\phi} \mathbb{E}_{q_{\phi}(z|x)}\left[\log p_{\theta}(x|z) \right] + \nabla_{\phi}KL(\dots)\\
&\approx \nabla_{\phi} \int q_{\phi}(z|x) \log p_{\theta}(x|z) dz \\
&\approx \int \nabla_{\phi}q_{\phi}(z|x) \log p_{\theta}(x|z) dz \\
&\approx \int q_{\phi}(z|x)\nabla_{\phi}\log q_{\phi}(z|x) \log p(x|z) dz \\
&\approx n \log p_{\theta}(x|z)\nabla_{\phi}\log q_{\phi}(z|x) \quad z \sim q_{\phi}(z|x)
\end{split}
$
推導過程中用上了一個技巧,稱為log-derivative trick
$$
\nabla_{\phi}\log q_{\phi}(z|x) = \frac{\nabla_{\phi}q_{\phi}(z|x)}{q_{\phi}(z|x)}
$$
所以可以把$\nabla_{\phi}q_{\phi}(z|x)$代換掉,得到一個能用抽樣近似的式子。所以總結一下上述的推導,$\nabla_{\theta}L(\phi,\theta)$是在訓練我們的生成模型,也可以說是Decoder,最大化$p_{\theta}(x)=p_{\theta}(x|z)p(z)$,這裡等同於EM演算法中的M步驟;而$\nabla_{\phi}L(\phi,\theta)$含有兩個部分,一個部分是KL的微分項,有解析公式容易計算,但另一項的積分就只能靠抽樣來近似,抽樣出$z$並計算對$\phi$梯度與資料似然加總,得到沒有偏差(Unbiased)的梯度估計
Reparametrization-based low-variance gradient estimator
上一小節我們得到了參數對於目標函數的梯度,但還有個問題,就是$\nabla_{\phi}L(\phi,\theta)$的變異(variance)非常的大,$n \log p_{\theta}(x|z)$有可能會是非常大的值而使得梯度過大;梯度是向量來描述要往哪邊走,才會使得目標函數最小,當變異很大時,就像是每個人都說要往不同的方向走,到最後這些方向加總在一起反而依然在原地打轉,或是有一個人說要往某個方向走非常大的一步,大過於其他人而造成梯度是有偏誤的,雖然期望上$\nabla_{\phi}L(\phi,\theta)$是個不偏估計,但是梯度變異過大使得訓練參數很困難
本篇論文的另一個重點就是用上Reparametrization trick於梯度估計上,提出一個低變異的梯度估計方法,才使得VAE能穩定訓練;我們將隨機的抽樣過程 $z \sim q_{\phi}(z|x)$,改成一個決定性的計算過程,例如要從高斯分佈中抽樣,我們可以改成
$$
z = g_{\mu, \sigma}(\epsilon) = \mu + \epsilon \cdot \sigma, \quad \epsilon \sim N(0,1)
$$
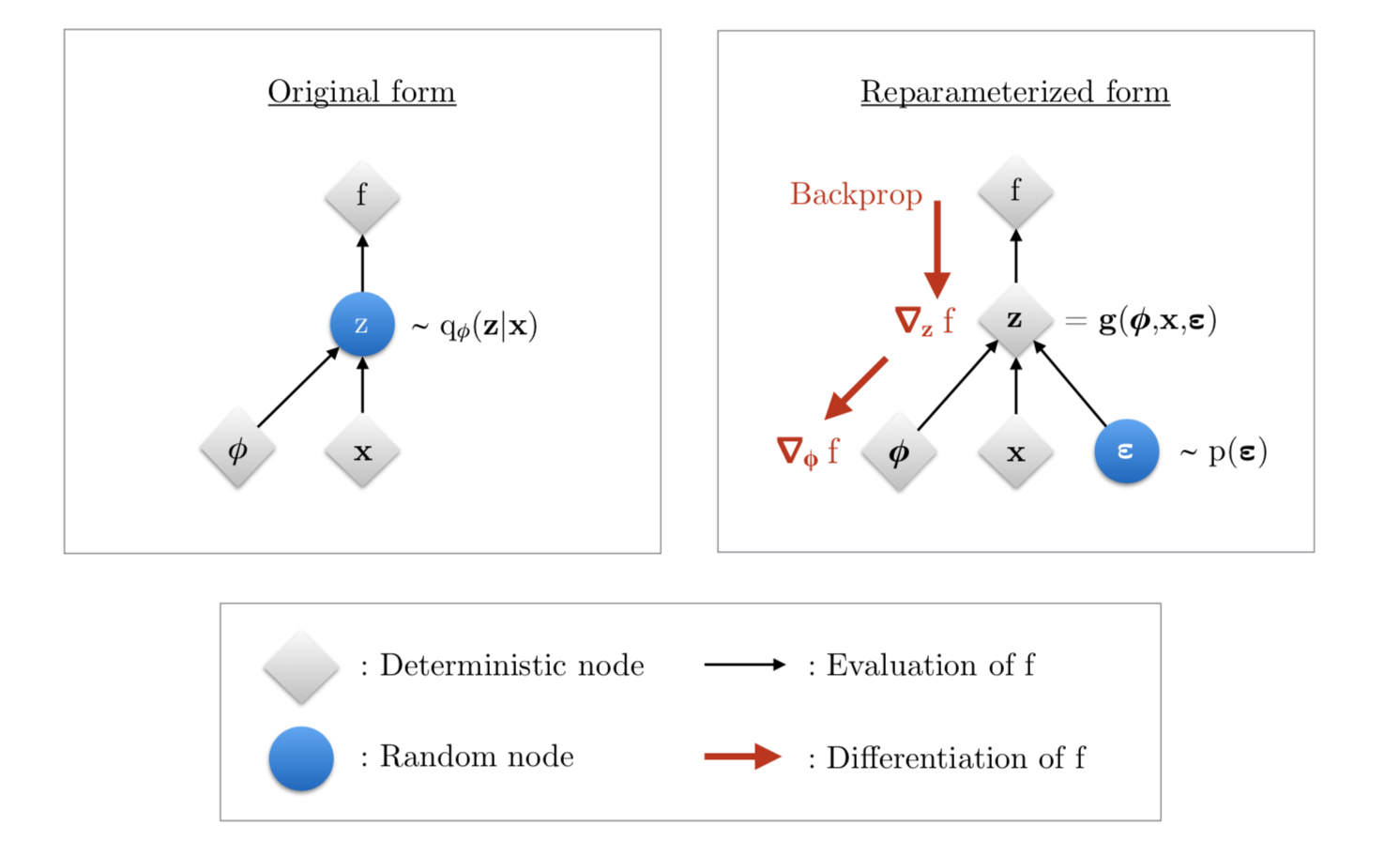
圖片來源:VARIATIONAL INFERENCE & DEEP LEARNING: A NEW SYNTHESIS
抽樣會使得梯度無法傳遞,就像左邊那張圖一樣,Z是一個隨機計算節點,經過Z後我們無法對之前的計算有任何資訊,自然也無法計算梯度,但改成Reparameterized form後,梯度就能順利回傳至參數上;另一點是有效減少梯度變異,原本梯度計算過程受$n \log p_{\theta}(x|z)$影響而造成變異過大,而現在我們只需要計算$\nabla_\phi f$的期望值,兩者數值大小差異很大,因此減少梯度變異使訓練過程穩定,才能用在複雜的資料集上
$$
\nabla_\phi \mathbb{E}_{z \sim q(z\mid x)}\left[ f(x,z) \right] = \mathbb{E}_{\epsilon \sim p(\epsilon)} \left[ \nabla _{\phi} f(x,g(\epsilon, x))\right]
$$
結語
本篇是漫談VI方法的第二篇,細談了VAE模型基礎,如何從ELBO對應到自編碼器架構,且$KL(q_{\phi}(z|x)||p(z))$也可以看成是一種正規化項,並提出改進的梯度估計方法,才能使得訓練模型成為可能,VAE是非常好的表徵學習方法,訓練穩定並能結合半監督式學習、增強學習等技術,後續很多的理論改進應用延伸,值得關注與學習
下一篇會討論VAE與其他生成模型的關係,最近有一些工作討論將各種生成模型放入同一個框架內討論,敬請期待