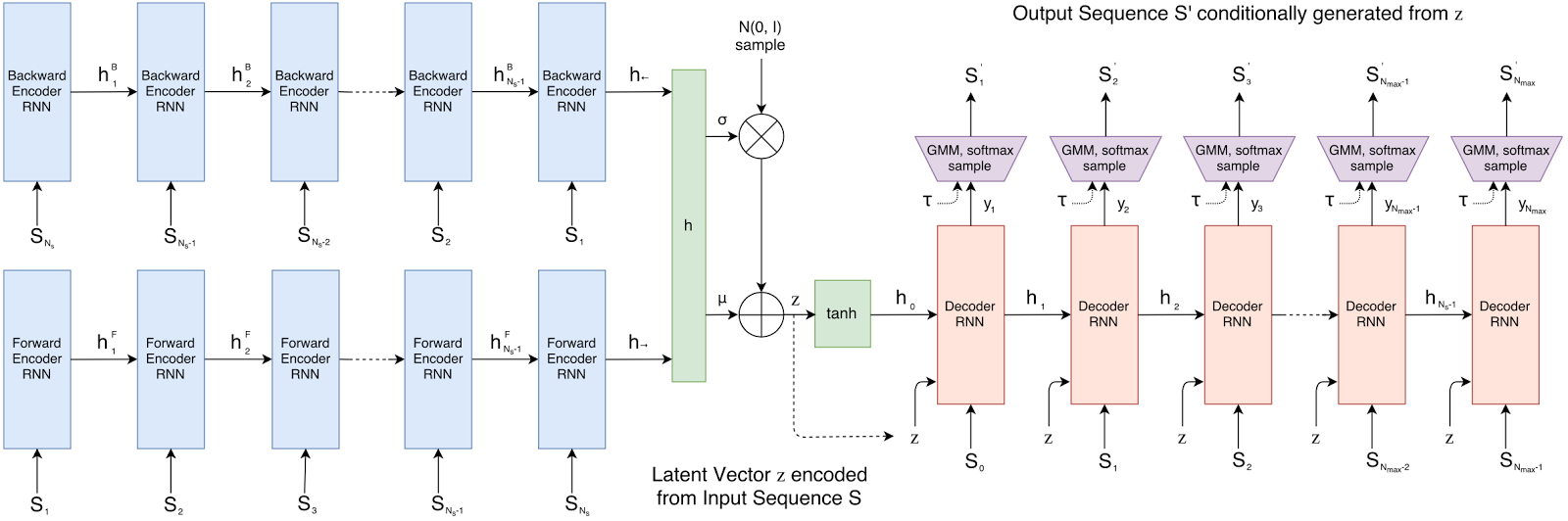
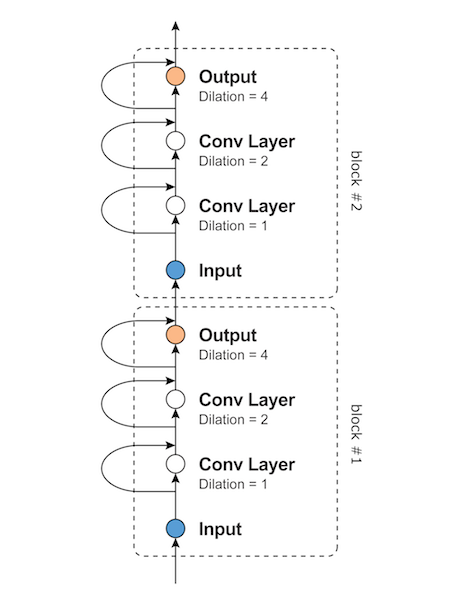
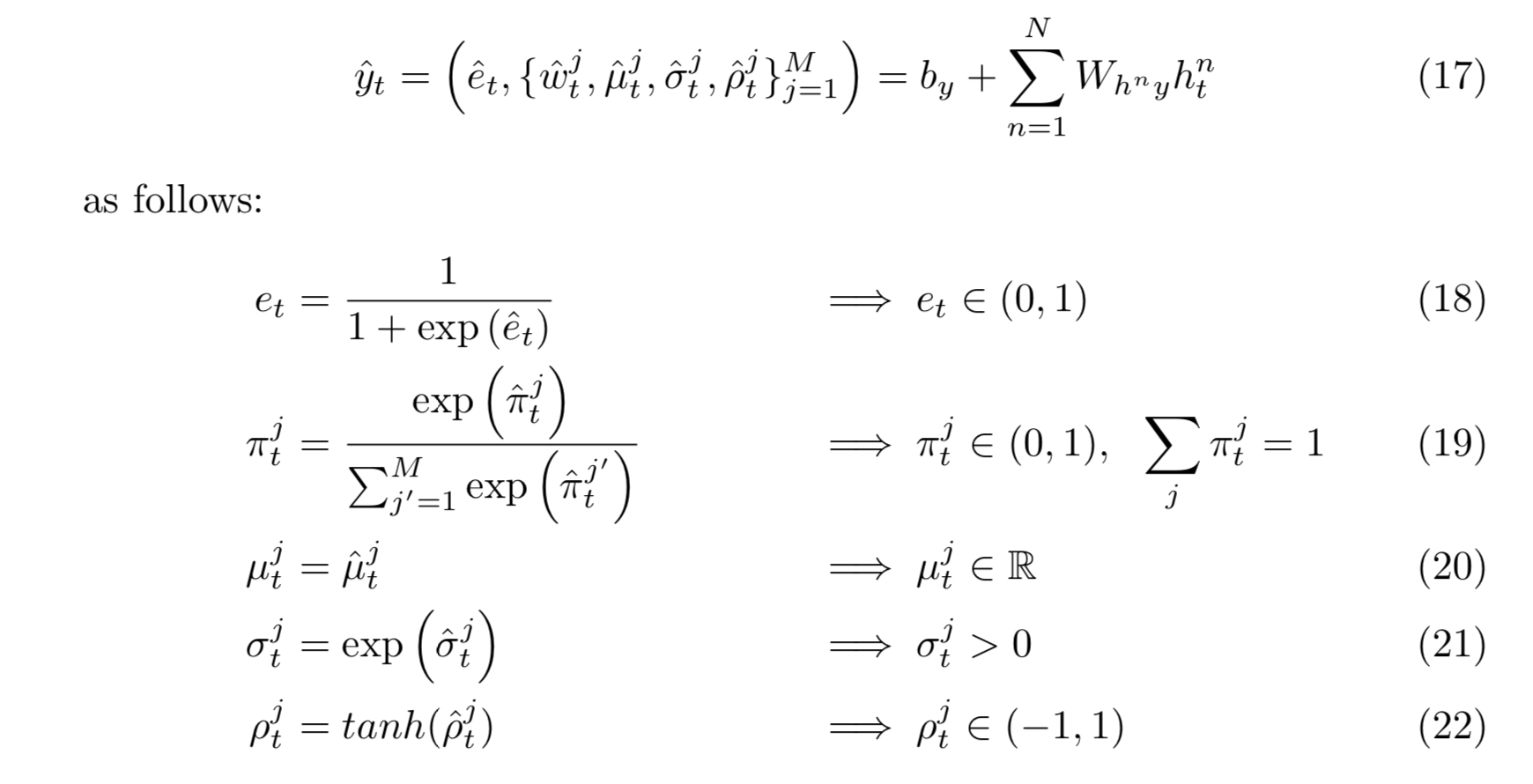Pyro 是一個由Uber AI Lab所開發的Probabilistic Programming Language(PPL)，用程式語言來描述具有隨機性的程序或是過程；從另一個角度來看，圖機率模型(PGM)是用圖的方式來描述一個機率過程，而PPL則是可以讓你用上程式語言來描述，條件、迴圈等等都可以用上，能描述更為複雜的機率過程

PPL也存在好一陣子了，像是MIT基於LISP所開發的Church、webppl都是，但都偏向是學術性的語言；隨著深度學習也用上了一些機率推斷方法，像是MCMC、Variational inference等，也出現基於Tensorflow、Pytorch框架的PPL，能更好的與深度學習方法結合，並且引入很多有用的機率數學工具

Introduction of Pyro

根據官網描述，Pyro有幾個特點

• Universal: Pyro can represent any computable probability distribution.
• Scalable: Pyro scales to large data sets with little overhead.
• Minimal: Pyro is implemented with a small core of powerful, composable abstractions.
• Flexible: Pyro aims for automation when you want it, control when you need it.

基於Pytorch開發，所以深度學習那些當然都可以整合一起用上，並且語法非常的Pythonic，也用上了很多高階特性，例如context manager，機率推斷演算法主要提供Stochastic Variational Inference(SVI)，可以用上SGD來訓練模型，整體上的確以最小需要、高彈性、透明為主要設計，相較於基於Tensorflow的Edward、Tensorflow_probability，提供不只VI相關演算法，還有很多MCMC相關的，或是前一篇提到的NF，更多工具可以使用，但也相對不是那麼容易上手；不過結合更多機率特性是趨勢之一，這兩個主流的Deep PPL都很值得關注與學習。

Implement LDA model

以上介紹了Pyro，接著就來實作Latent Dirichlet allocation(LDA)模型，常用文本主題分析，且為圖機率模型的經典模型！接著用Pyro與SVI來實作並求解參數，本文並不會從頭介紹Pyro基礎，建議可以先看官網教學，程式碼我放在Colab，大家可以直接跑看看

Model

我們就直接從模型看起，先來看一下LDA式子長怎樣，$\phi$指每個字對應個主題的機率分佈，$\theta_d$指每一文件對應主題的機率分佈，$z$指每個字被分配到的主題，式子可以寫成：

$$
p(\phi,\theta,z,w) = p(\phi) \prod_{d=1}^D \prod_{n=1}^{N_d} p(z_{dn}|\theta_d)p(w_{dn}|z_{dn},\phi)
$$

式子對應Pyro程式碼如下：

1
2
3
4
5
6
7
8
9
10

@pyro.poutine.broadcast
def model(data):
  phi = pyro.sample("phi",dist.Dirichlet(torch.ones([K, V])).independent(1))
  
  for d in pyro.irange("documents", D):
    theta_d = pyro.sample("theta_%d"%d, dist.Dirichlet(torch.ones([K])))
    
    with pyro.iarange("words_%d"%d, N[d]):
      z = pyro.sample("z_%d"%d, dist.Categorical(theta_d))
      pyro.sample("w_%d"%d, dist.Categorical(phi[z]), obs=data[d])

Guide

$w$是已知觀測變量，想要估計的隱變量有$\phi,\theta,z$，我們可以用上Variational inference方法來最大化資料似然$\log p(w)$，並用另一個guide來近似$p(\phi,\theta,z|w)$，有關於VI相關會在後續寫個幾篇好好來講講

$$
q(\phi,\theta,z) = q(\phi) \prod_{d=1}^D q(\theta_d)\prod_{n=1}^{N_d} q(z_{dn})
$$

式子對應Pyro程式碼如下：

1
2
3
4
5
6
7
8
9
10
11
12
13

@pyro.poutine.broadcast
def guide(data):
  beta_q = pyro.param("beta_q", torch.ones([K, V]),constraint=constraints.positive)
  phi_q = pyro.sample("phi",dist.Dirichlet(beta_q).independent(1))
  
  for d in pyro.irange("documents", D):
    alpha_q = pyro.param("alpha_q_%d"%d, torch.ones([K]),constraint=constraints.positive)
    q_theta_d = pyro.sample("theta_%d"%d, dist.Dirichlet(alpha_q))
    
    with pyro.iarange("words_%d"%d, N[d]):
      q_i = pyro.param("q_%d"%d, torch.randn([N[d], K]).exp(),
                       constraint=constraints.simplex)
      pyro.sample("z_%d"%d, dist.Categorical(q_i))

注意guide裡面有參數是需要訓練的，比如每一個字所對應的$z_dn$，我們都用一個Categorical分佈來代表主題，都有參數需要訓練，很直接去估文件裡的每個字代表什麼主題

Training

最後用SVI去最大化ELBO

1
2
3
4
5
6
7

adam_params = {"lr": 0.01, "betas": (0.90, 0.999)}
optimizer = Adam(adam_params)

svi = SVI(model, config_enumerate(guide, 'parallel'), optimizer, loss=TraceEnum_ELBO(max_iarange_nesting=1))

for _ in range(3000):
  loss = svi.step(data)

TraceEnum_ELBO適用於有離散變量需要估計的時候，會直接去做enumerate，不然單用Trace_ELBO遇到離散變量效果都很差

Result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

pyro.param('q_2')
>>>
tensor([[0.8072, 0.0559, 0.0606, 0.0543, 0.0220],
        [0.9249, 0.0258, 0.0146, 0.0242, 0.0104],
        [0.9250, 0.0258, 0.0145, 0.0243, 0.0105],
        [0.3842, 0.0408, 0.5215, 0.0381, 0.0153],
        [0.9406, 0.0206, 0.0110, 0.0193, 0.0085],
        [0.9406, 0.0206, 0.0111, 0.0193, 0.0084],
        [0.9406, 0.0204, 0.0110, 0.0192, 0.0088],
        [0.9406, 0.0205, 0.0111, 0.0193, 0.0085],
        [0.9250, 0.0258, 0.0145, 0.0242, 0.0105]], grad_fn=<DivBackward1>)
        
z[2]
>>>
tensor([0, 0, 0, 0, 0, 0, 0, 0, 0])

看一下第二筆文件裡的字，估計主題效果還不錯

1
2
3
4
5
6
7
8
9
10

phi[0]
>>>
tensor([1.1714e-03, 7.1110e-01, 1.4448e-03, 1.8015e-03, 1.0734e-01, 2.6613e-06,
        1.1921e-07, 3.6218e-03, 9.7121e-02, 1.1921e-07, 8.0717e-03, 7.9834e-07,
        6.8322e-02, 1.1921e-07, 1.1921e-07])

dist.Dirichlet(pyro.param('beta_q')).sample()[0]
>>>
tensor([0.0089, 0.4932, 0.0083, 0.0549, 0.1486, 0.0355, 0.0272, 0.0291, 0.0509,
        0.0098, 0.0045, 0.0631, 0.0331, 0.0021, 0.0308])

來看第1個主題對應字的機率，都是第2個字的機率最高，代表主題1最相關的字為第2個，雖然分佈可能還有點差異，但效果也還不差

結語

深度學習結合機率方法是趨勢，這些PPL框架能更快投入研究與產品，後續會再分享一些Pyro應用與心得

機率分佈估計一直是機器學習中的核心問題，不論是分類問題估計條件機率分佈$p(y|x)$，或是建立生成模型$p(x,z)$，我們都在從資料中建立與學習出一個機率分佈

基本上機率分佈能做到兩件事：

• 評估機率值，計算$p(x)$，給樣本空間的點都要能得出機率值
• 抽樣，計算$x \sim p(x)$，要能依機率密度來抽樣出樣本

近年來，深度學習能有效率的近似高維度的複雜函數，而且還有完整的訓練框架，再加上機率圖模型概念，能表示很多複雜的機率分佈，但雖然能訓練模型來估計複雜分佈，也不一定能做到上面說的兩件事，比如：GAN很容易生成新影像，但卻無法給一張影像估計其機率值

Normalizing Flows是一種能將機率分佈轉換到另一個分佈的數學工具，例如把簡單的高斯分佈轉換至另一個複雜的機率分佈上，且依然能有效率評估機率值與抽樣，最近很多論文也開始結合這類的方法，例如：

• Improving Variational Inference with Inverse Autoregressive Flow
• Masked Autoregressive Flow for Density Estimation

還有最近由OpenAI剛發佈的Glow: Generative Flow with Invertible 1x1 Convolutions，基於Normalizing Flows的一種生成模型，也能生成高品質影像與表徵解構

Normalizing Flows

假設隨機變量$x \in \mathbb{R}^d$且$x \sim p(x)$，與一個可逆函數$f:\mathbb{R}^d \mapsto \mathbb{R}^d$，我們用$f$來轉換$p(x)$，可以得到另一個經過轉換的隨機變量$y=f(x)$與其機率分佈：

$
p(y) = p(x) \left|
\mathrm{det} \frac{
\partial f^{-1}
}{
\partial x
}
\right|
= p(x) \left|
\mathrm{det} \frac{
\partial f
}{
\partial x
}
\right| ^{-1} \tag{1}
$

行列式直觀上是面積或是體積的縮放比例，機率為機率密度函數底下的面積，轉換函數$f$可是視為一種面積的縮放變形，所以$p(y)$由轉換前$p(x)$底下的面積，乘上行列式表示的面積縮放比例，因為是計算$f^{-1}$，這個面積縮放的比例係指$y$對於$x$影響，意思是說，給$y$來反推回去$x$，並調整$p(x)$底下的面積大小，但也可以計算向前過程的行列式來取倒數。

假設轉換由多個轉換函數$f_1 \dots f_K$組成，$z_k$為轉換過程的中間變量，最後得到的隨機變量$y = f_K \circ \dots\circ f_1(x)$，計算$\log p(y)$為：

$
\log p(y) = \log p(x) - \sum_{k=1}^K
\log
\left|
\mathrm{det} \frac{
\partial f_k
}{
\partial \mathbf{x}_{k-1}
}
\right| \tag{2}
$

綜上所述，NF有兩種計算，第一是向前抽樣計算，從$x$計算$y = f(x)$，第二是向後機率機算，給一個$y$要一步步往後做逆運算，計算轉換的行列式總和，最後求出$x$。

計算行列式最差時候需要$O(n^3)$，所以就需要設計比較容易計算行列式的轉換，例如 Masked Autoregressive Flow、Inversed Autoregressive Flow、RealNVP等等模型，有用到Autoregressive的特性，所以行列式會很容易計算，這些方法會在後續的文章中介紹。

Training and sampling

向後機率計算，我們可以直接對$\log p(y)$最大化機率似然，給$y$透過一系列反函數得到$x$與行列式總和

$$x = f_1^{-1} \circ \dots \circ f_K^{-1}(y)$$

最後計算$\log p(x)$減去轉換過程行列式總和(如式子2)，就可以算出$\log p(y)$，當然也就能用上SGD等優化方法，一系列轉換函數就當成一層層神經網路來訓練，只是這裡要求要能計算反函數

向前抽樣計算，出新樣本很直觀，就從$p(x)$抽樣出$x$，經過轉換即可得到$y$，而且還能順便得到$p(y)$

$$y = f_K \circ \dots \circ f_1(x)$$

如果對NF有興趣，參考資料都很值得一看！

之後會放上一個實作例子，把簡單機率分佈轉換至一個複雜分佈，還有關於最近NF發展的論文的閱讀心得

Reference

1. Normalizing Flows Tutorial by Eric Jang
2. Normalizing Flows by Adam Kosiorek
3. Improving Variational Inference with Inverse Autoregressive Flow
4. Variational Autoencoders with Inverse Autoregressive Flows

之前Google有一個有趣的小遊戲Quickdraw，給你一個題目要你20秒內畫出來，當然除了讓你打發時間外，大家手繪大作也變成機器的精神糧食，拿來學習了XD

SketchRNN是一個向量軌跡的生成模型，這篇部落格文章可以看到很多有趣的結果，詳細的模型架構與訓練過程可以看這一篇論文

整個模型可分為3個部分：

• Seq2seq autoencoder + Gaussian mixture model
• Variational inference

Seq2seq autoencoder + Gaussian mixture model

Seq2seq+GMM這是很經典的序列至序列架構，最早是出現在這一篇Generating Sequences With Recurrent Neural Networks，並且有一個手寫筆跡產生的應用，也算是這個塗鴉的前身之作，作者是Alex Graves，他可是Hinton的博士生喔！

架構上是一個序列至序列模型，$encoder$是雙向的LSTM，每個時間點吃入筆跡$x,y$實數座標值與下筆狀態類別，而$decoder$是單向的LSTM，每個時間點輸出下一個時間點的筆跡座標與下筆狀態

下筆狀態是離散的類別，這個很容易處理，只是簡單的分類問題，用個$softmax$就搞定了，輸出就是離散類別的機率分佈，但是連續資料我們要怎麼處理呢？怎麼建立連續的機率分佈呢？

我們常用高斯分佈是來作為連續變量的機率分佈，每個時間點可以輸出$\mu,\sigma$來建立高斯分佈，但對於複雜的資料，只用一個高斯分佈可能太過簡單，無法很好的捕捉資料的分佈，例如：筆跡座標可能有蠻大的變異性，很難說每個時間點就只用一個高斯就能代表，畢盡畫圖很隨性的呀～

所以用上GMM來增加輸出的機率分佈複雜度，由多個高斯分佈組合起來，形成一個複雜的機率分佈，如圖，用上3個不同參數的高斯分佈，就能組合出紅色的這個複雜分佈

每個時間點模型給出的預測$\hat{y}$為公式17，分別為是否停止、GMM的參數等，就可以直接做MLE訓練

Variational inference

VAE這個東西是一個非常熱門的生成模型，下次有機會再開一篇來講講，如果想簡單了解，可以直接看這裡，直觀上SketchRNN透過$encoder$把序列壓縮到一個連續空間中，這個連續空間為高斯分佈$N(0,1)$，而$decoder$要能還原回原本的軌跡，但我們能從連續空間中抽樣出新的點，由$decoder$產生軌跡，就是產生新的塗鴉囉！

Implement and Tricks

我的實作版本，以Pytorch實作

Data processing & Training

• quickdraw-dataset有約300多種類別的塗鴉資料可以下載
• 軌跡都是正整數，要先剔除一些異常資料，再做縮放正規化，這部分可以參考實作
• Google實作還有做一些data augmentation，有些類別資料很少，但我實作裡沒有
• 訓練就跟一般seq2seq差不多，而且蠻快的
• 產生新樣本時，不論是直接從高斯抽樣，或是從給定的序列去還原，有一個部分要特別注意，就是tempture，調整tempture會改變輸出的機率分佈，低的溫度會使分佈更為集中，高的反之亦然，溫度低筆觸就不會到處亂飄，因為機率分佈集中了，比較容易畫出像樣的圖，而溫度高，分佈就比較均勻，筆觸就容易到處飄，就不容易畫出好的圖

Reference

1. Teaching Machines to Draw
2. A Neural Representation of Sketch Drawings
3. magenta/models/sketch_rnn
4. alexis-jacq/Pytorch-Sketch-RNN

WaveNet: A Generative Model for Raw Audio 是 DeepMind所提出的一種用於聲音的生成模型，例如最近發布的CLOUD TEXT-TO-SPEECH用的模型架構就是以這個為基礎，還有Making a Neural Synthesizer Instrument裡面都有用上類似WaveNet的結構

Autoregressive model

統計上常用來處理時間序列的方法，用過去歷史資料 $x_{1:t-1}$來預測現在$x_t$，可以看成過去的自己對現在的自己做回歸，所以被稱為自回歸模型

本模型也是用過去的聲音訊號來預測現在的訊號點，這樣的缺點是要生成新樣本的時候效率很差，因為資料有序列關係，總是要等待前面產生，才可以依序產生新的點，算是這類模型的問題

Fully observed model

本模型沒有任何的Latent variable，沒有需要估計或是近似的未知變量，任何資訊都是完全可見的，都是從過去歷史資料來的，這樣的模型架構上更為直接簡單，不需要處理隱變量問題，用上繁瑣的近似演算法等等，而可以直接做MLE訓練

Implement and Tricks

我的實作版本，以Pytorch實作，僅有針對單一人語音訓練，沒有做多人訓練或是TTS等，但實作上相對透明簡單，可以比較深入看看實作過程

Causal & Dilated Conv1d

圖片來源：WaveNet: A Generative Model for Raw Audio

• Causal:不能用到未來的資訊，例如在實作 PixelCNN時，要把Kernel的一部分mask起來，但是在本實作1D conv時，Kernel直接是2，意思為要預測$x_{t}$時，僅用到$x_{t-2}$與$x_{t-1}$，不過要記得把最後一個時間去掉
• Dilated: 讓Kernel看遠一點，不要只看鄰居，如果Dilated設定大一些時，就會看$x_{t}$與$x_{t-N}$，大幅增加視野域，我猜音訊鄰近的時間點值都差不多，不如看遠一點可能會有比較多變化，提供模型更多有用訊息；建議參考這篇來了解Dilated Conv

Residual & Stack block

圖片來源：ご注文は機械学習ですか

圖片來源：WaveNet: A Generative Model for Raw Audio

• 模型以多個Block堆疊在一起，每個Block含有多個Dilated Conv，並且加入Residual link來幫助梯度傳遞
• 把每一個Block的輸出匯集並加起來，每個Block計算視野不同，越往上層越大，代表資料不同的resolution，最後加總在經過轉換輸出得到下一個時間點的預測

Data processing & Training

• VCTK資料集有多人的語音與文字內容，可以用來訓練TTS系統
• 語音資料處理我用上torchaudio、librosa，但不知道為什麼用兩個套件讀出來的有點差異，我最後用librosa來讀取音訊，還有把無聲部分去掉，這個步驟非常重要！不然訓練到最後只會一直產生靜音，再用torchaudio做Mulaw encoding
• 訓練batch size為1，一次給一段語音來訓練，基本上因為訓練資料長度差異很大，要做padding很浪費與不好做，再且顯卡記憶體也不夠大，所以一次訓練一個語音檔是合理的做法
• 訓練大概要2天，而且頗慢的，建議做learning rate scheduling從0.001往下到0.00001，我訓練在p225這個語音上，最後得到loss約2左右，可以得到還可以的結果
• 計算視野其實蠻簡單，就餵給模型資料來測試看多長的資料，模型剛好輸出為1，就是模型的視野，代表要預測下一個時間點，需要往前看多長的資料
• 產生新樣本非常慢的，請耐心等待，所以這一篇頂多只能說是開一個研究開頭，而且也無法直接做到TTS或其他應用，而是一個好的音訊產生網路結構，後續很多聲音產生都是基於此

Reference

1. Sergei Turukin blog
2. winter plum blog
3. ご注文は機械学習ですか