最近在研究基於能量或是梯度的生成模型,在生成的過程都會需要用到抽樣方法,來從模型學習到的分佈中抽樣出樣本,如何於高維度的空間中抽樣是一個重要問題,例如 Markov chain Monte Carlo 這類演算法,是基於建構一個狀態轉移矩陣來得到一個平穩分佈,最後可以從平穩分佈中來抽樣出樣本,網路上有很多好文章講解 MCMC,雖然在一般常見的深度學習任務中,並不常用 MCMC 來求解積分或是抽樣,但是依然是一個很重要且值得學習的方法
Langevin Dynamics 抽樣方法是另一類抽樣方法,不是基於建構狀態轉移矩陣,而是基於粒子運動假設來產生穩定分佈,MCMC 中的狀態轉移矩陣常常都是隨機跳到下一個點,所以過程會產生很多被拒絕的樣本,我們希望一直往能量低或是機率高的區域前進,但在高維度空間中單憑隨機亂跳,很難抽樣出高機率的樣本,所以如果我們能引入梯度或是一些粒子運動假設,能幫助我們知道高機率的區域應該往哪裡,這樣便可以大幅加速我們抽樣的效率與品質;之前在很多論文中就常看到這個抽樣方法被使用,單看公式非常像梯度下降演算法,只是更新梯度前乘上一個係數並且多加上了一個隨機項,這樣竟然就可以變成一個抽樣方法,優化跟抽樣能一起做,覺得非常神奇,本篇文章是 Langevin Dynamics for sampling and global optimization 的學習心得,底下的圖也都是來自於投影片,但因為內容涉及隨機微分方程,我沒有系統性的學習過,所以僅是整理一下整個 Langevin Dynamics 抽樣方法的概念,數學推導可能不夠嚴謹,如果觀念上有錯誤也請大家不吝指教囉!
Langevin Dynamics

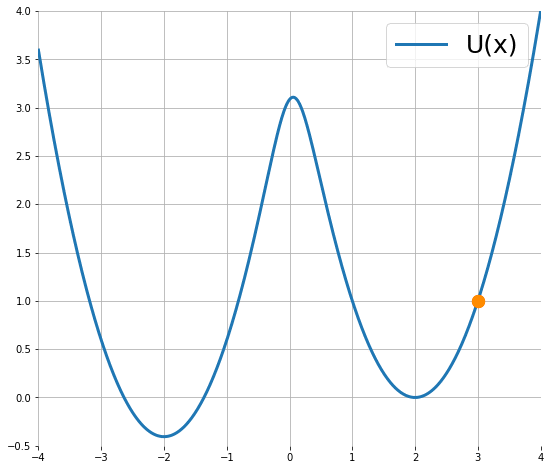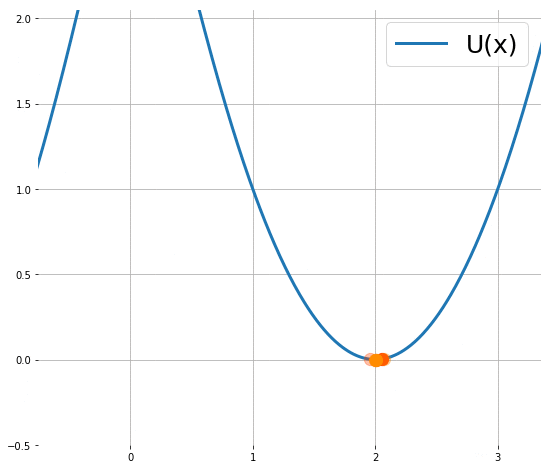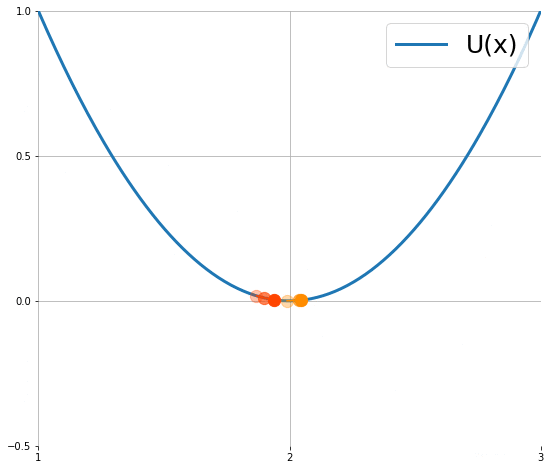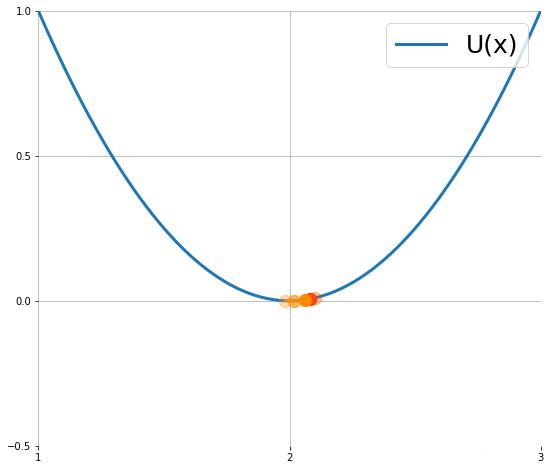
Langevin Dynamics 用隨機微分方程描述了粒子移動,粒子的移動隨著所在位置對能量函數的梯度與隨機項來決定,粒子當下位置$x$可由上一個位置$x’$來形成一個常態分佈所抽樣出來,像是下圖動畫顯示了粒子的運動過程
Fokker-Planck equation
基於上節的運動假設,在某個時間點粒子出現在空間中的的機率,我們可以用 Fokker-Planck equation 來描述,由上一個微小時間點$x’$的位置分佈來計算出特定時間點$x$的位置分佈
$$p(x, t)=\int d x^{\prime} p\left(x, t \mid x^{\prime}, t-d t\right) p\left(x^{\prime}, t-d t\right)$$
粒子的位置分佈會隨時間演化,最終形成一個穩定分佈 (紅色的線),而這個穩定分佈的樣子跟能量函數有關係
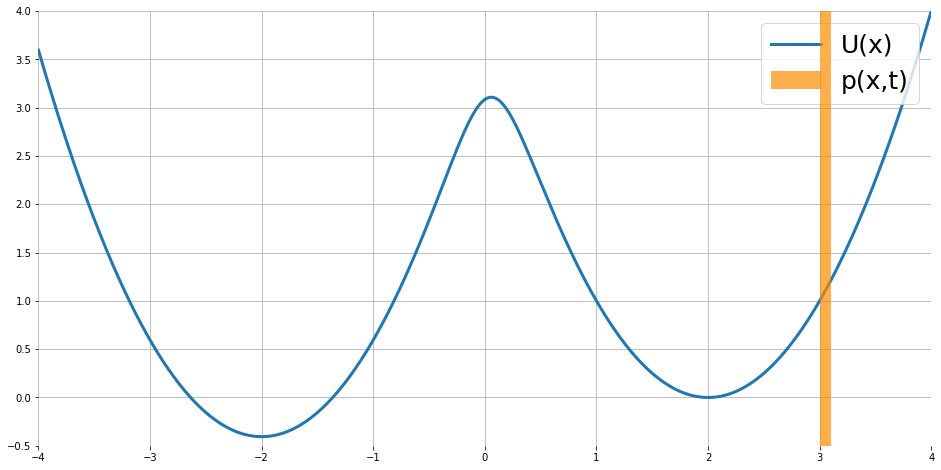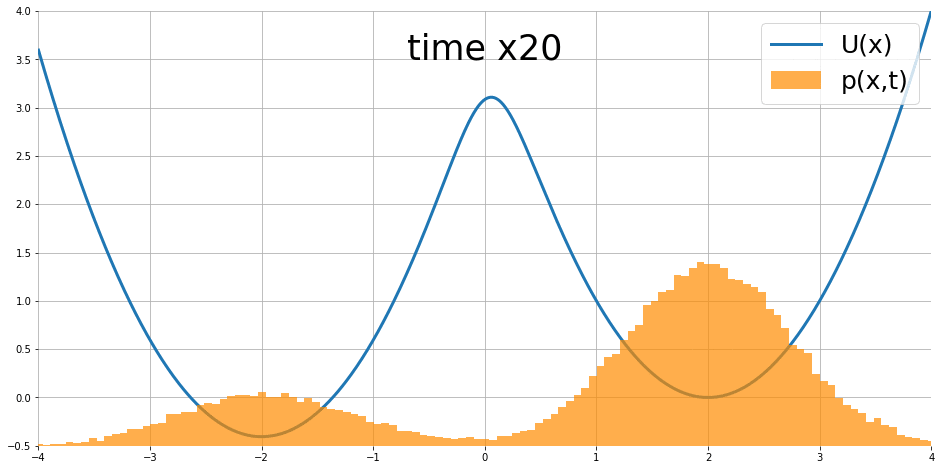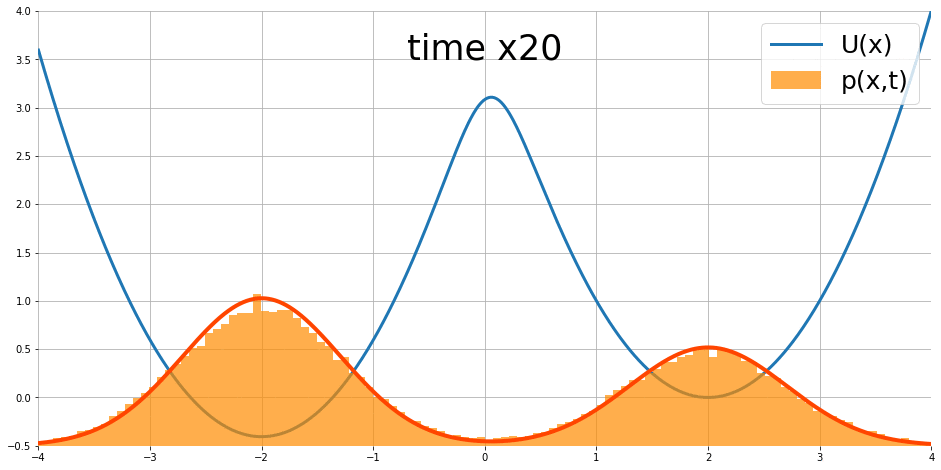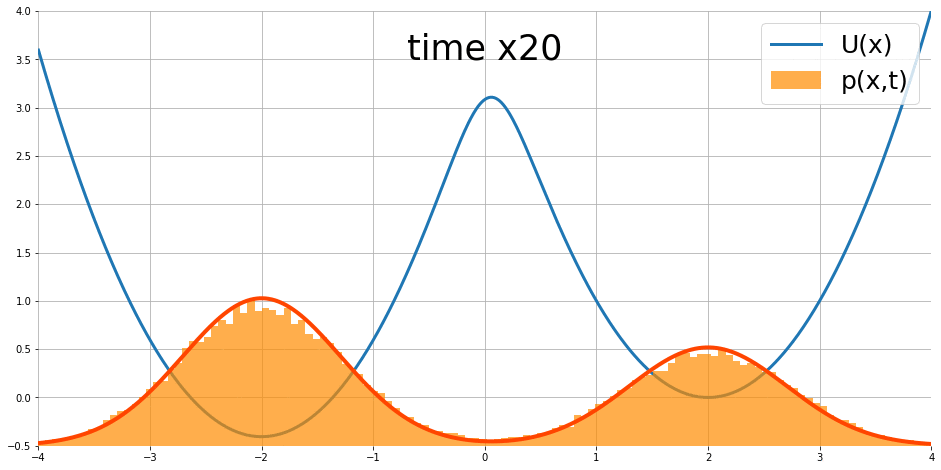
Stationary distribution
我們可以對 Fokker-Planck equation 微分,代表這個機率函數變化的梯度,如果當機率函數不在變化時,也就意指為穩定分佈,求解微分的過程蠻複雜的,用到很多數學技巧,我這邊就不細講,有興趣的人可以自行參考錄影與投影片

第一行就是最後得到的微分公式,我們假設穩定分佈可以寫成 $P_G(x)$,帶入得到的微分公式且當微分為0時,我們就解出 $P_G(x)$裡的 $T$,故之後我們只要知道能量函數 $U(x)$,就可以馬上知道穩定分佈的樣子
Sampling via the Langevin dynamics
我們知道依照 Langevin Dynamics 最終粒子出現的機率會是一個穩定分佈,如果這個穩定分佈恰好是我們設定或是想要的,那穩定後粒子的運動過程就等於抽樣
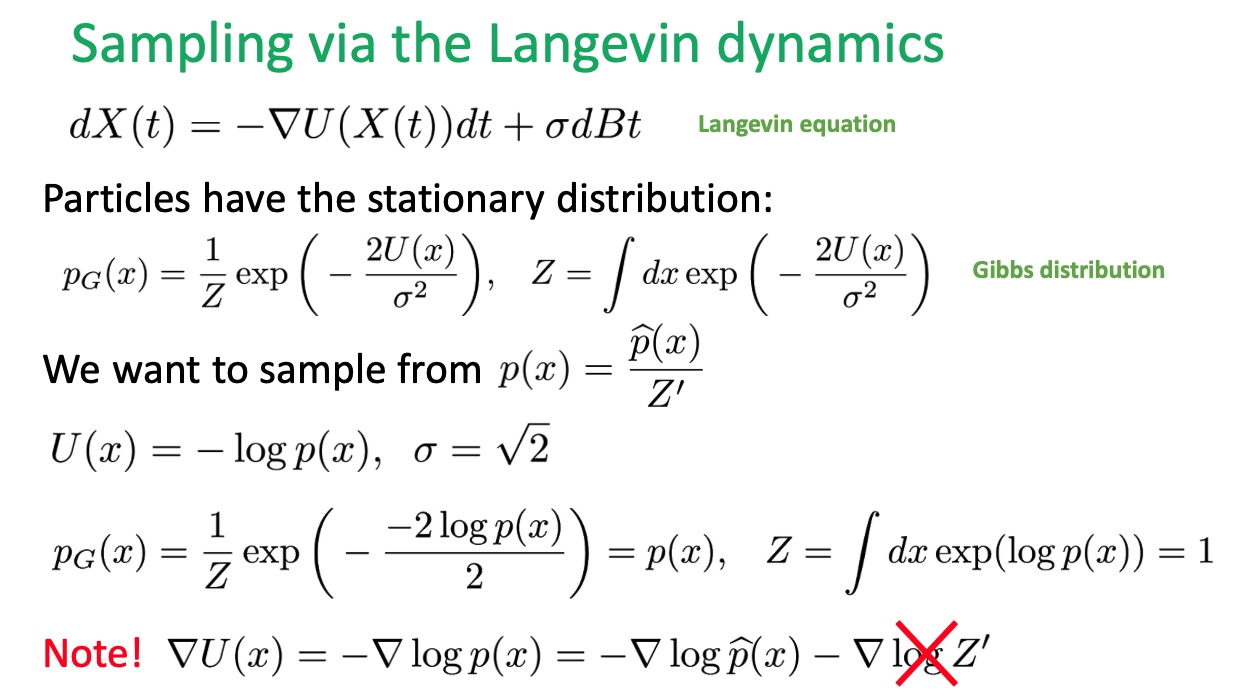
我們希望從 $p(x)$ 來抽樣出樣本,就是希望穩定分佈最後演化成這樣,我們要讓 $p_G(x) = p(x)$,故得到 $U(x) = - \log p(x)$ 與 $ \sigma=\sqrt{2} $ ,所以帶回去我們的運動假設中
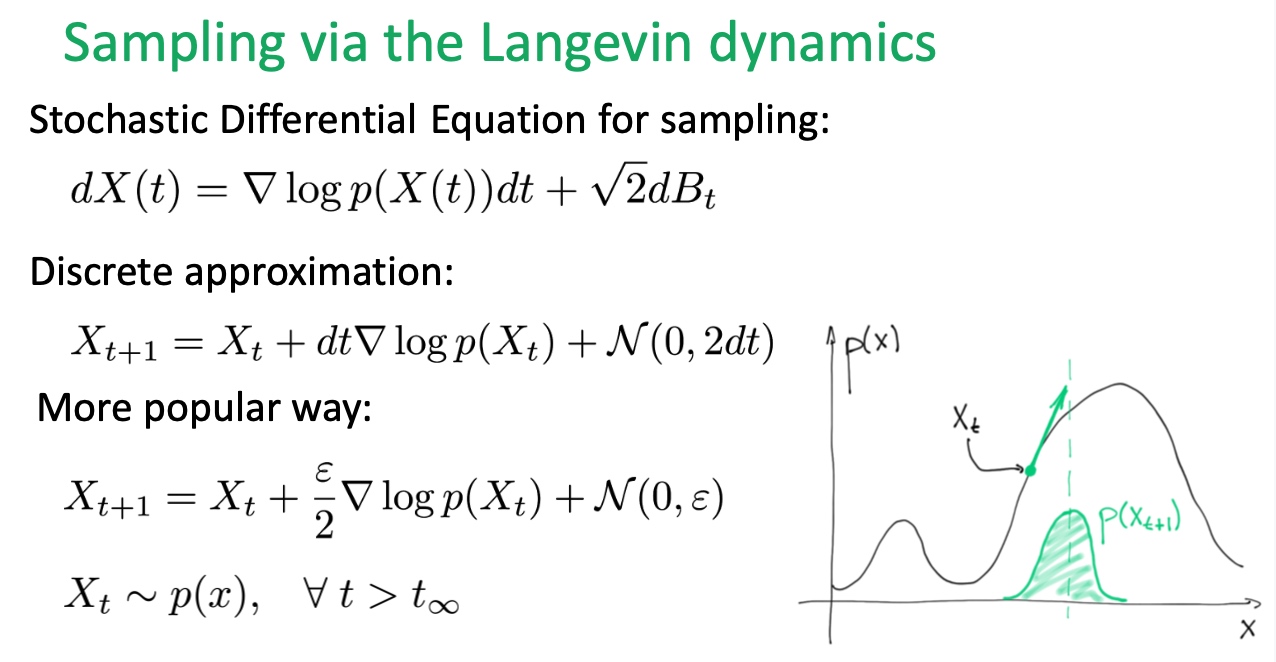
我們終於得到了使用 Langevin dynamics 進行抽樣的方法
結語
本文章我們稍微了解了使用 Langevin dynamics 來進行抽樣背後的原理,雖然抽樣方法可以直接當作工具去使用它,而不用管背後的原理,但是深入理解背後的原理也是相當有趣,很佩服這些受物理啟發的工作,後續我會分享一些生成模型的實作,並使用 Langevin dynamics 抽樣方法,敬請期待!