之前漫談了 Variational Inference ,基本上從機器學習與機率分佈近似的角度出發來談了理論與應用,我們旨在最小化ELBO,來最大化對於資料的解釋,而且從中學習到隱變量,且隱變量還能捕捉到資料潛在資訊,這樣的演算法非常精緻優雅,是我個人非常欣賞的模型;我們的大腦,或是更廣泛來說,一個需要與環境交互的生物或自組織系統,隨時都在對抗失序(resisting a tendency to disorder),生命需要維持一定的秩序才能生存,各種生理運作都必須精準穩定維持某種秩序,簡言之,維持穩定是生存的要務之一。
對於大腦來說,所謂的穩定就是對於各種輸入大腦都能給予解釋,大腦討厭surprise!大腦討厭無法解釋的東西,或是與自己預期差異很大的狀況,所以大腦的任務就是解釋或是預測各種輸入,來減少遇到surprise,這個概念為 The free energy principle。
The free energy principle 跟 Variational Inference 非常有關係,核心數學概念是相同的,由Karl Friston於2005提出,2010年於Nature上有一篇完整的概念描述 The free-energy principle:a unified brain theory ?,本篇會基於此文章來跟大家介紹這個概念;另外,2017年 Rafal Bogacz 寫了一篇 A tutorial on the free-energy framework for modelling perception and learning,這篇帶領讀者入門一些計算細節,本系列會基於這兩篇文章內容與大家分享。
The free energy principle
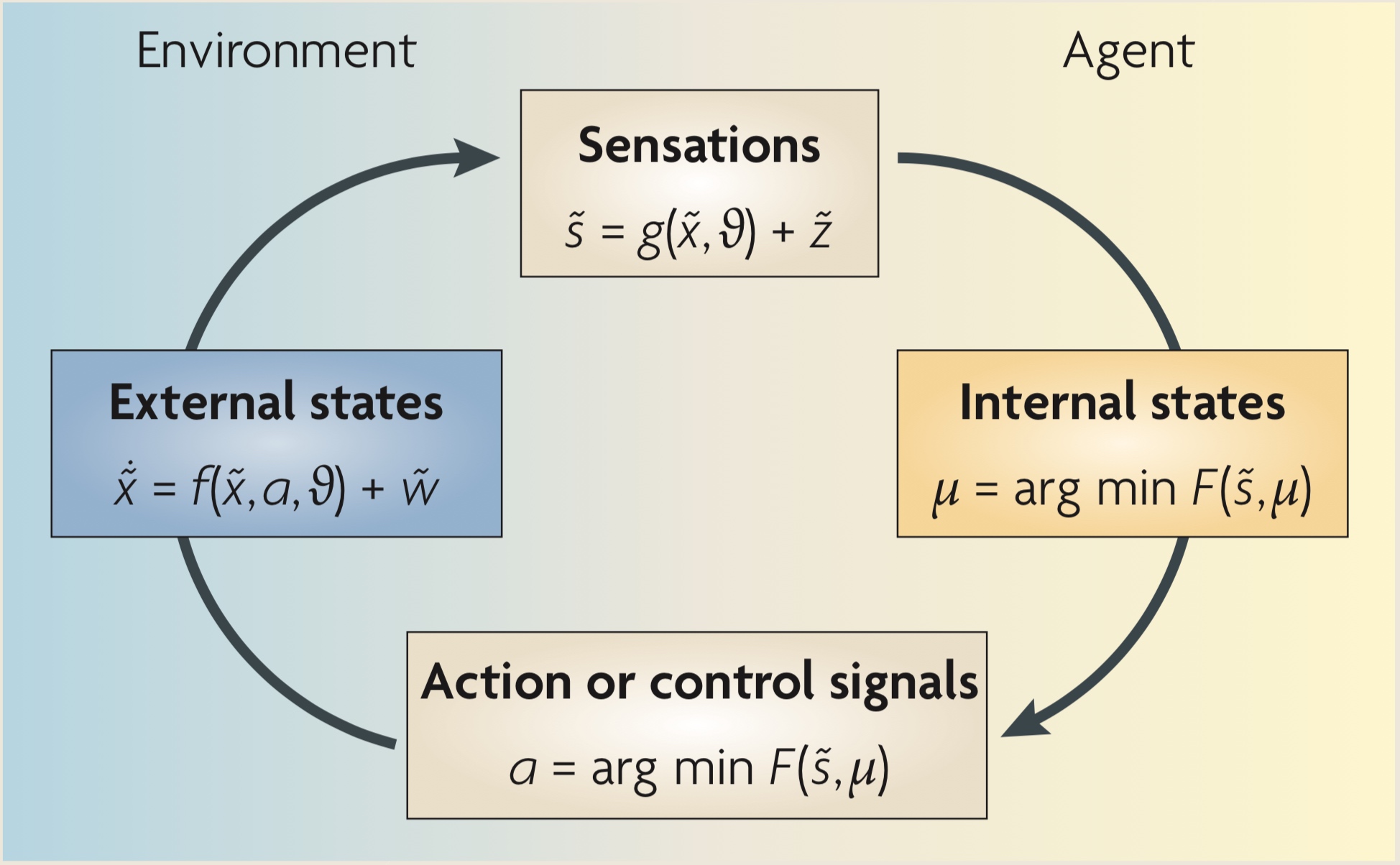
- 外部狀態(External states):會依agent產生的action與隱變量$\vartheta$改變,同時受到隨機干擾$\tilde {w}$的影響
- 感知(Sensation):觀測外部狀態$\tilde{x}$與隱變量$\vartheta$得到感知$\tilde{s}$
- 內部狀態(Internal states):最小化Free energy得到最佳的解釋$\mu$
- 決策行為:最小化Free energy來得到最佳的行為$a$
整個流程是一個動態的過程,每個變數都有初始值,透過這樣的循環,agent可以最大化對於環境狀態的了解,內部狀態$\mu$一開始可能完全是隨機的,但透過感知與行為來最小化Free energy,最後內部狀態會從外部狀態中獲取最多資訊
Free energy
其實Free energy就是我們之前提到過的ELBO,差異在於負號,我們希望最小化Free energy,而要最大化ELBO,不過其實從優化角度來看其實一樣
回顧一下ELBO,並且寫成另一個形式
$$
\begin{split}
\mathbb{E}_{q_{\phi}(z)}
\left[
\log \frac{p_{\theta}(x,z)} {q_{\phi}(z)}\right] &= \mathbb{E}\left[ \log p_{\theta}(x|z) \right] - KL(q_{\phi}(z) || p(z)) \\
&= \mathbb{E}\left[ \log p_{\theta}(x,z) \right] - \mathbb{H}\left[ q_{\phi}(z) \right]
\end{split}
$$
上述是以ELBO的角度,需要最大化ELBO,換到Free energy就加上負號,得到下圖的公式,接下來的描述也是以圖上的符號來說明:

Free-energy bound on suprise
- $q(\vartheta | \mu)$ 係指給定內部狀態解釋$\mu$對環境隱變量$\vartheta$的條件機率,跟VI想法一樣,我們無法精確知道隱變量的分佈,只好用一個近似的分佈來估計,所以我們如果對環境有好的解釋,我們應該可以把隱變量估計得比較好
- $p(\tilde { s } , \vartheta|m)$ 給定目前模型$m$,生成$\tilde{s},\vartheta$聯合機率分佈
- 可以對照上述ELBO式子,是完全對應的,整個Free energy 可以寫成 $F ( \tilde { s } , \mu )$,我們可以分別針對兩個變量來最小化
Perception optimizes predictions
- $\mu = \arg \min F ( \tilde { s } , \mu )$
- 根據現在輸入的感知,調整內部狀態$\mu$來最小化$F$,這個跟VI做的事情一樣,去學習好的表徵
Action minimizes prediction errors
- $a = \arg \min F ( \tilde { s } , \mu )$
- 這裡就是有趣的地方了,其實除了可以透過改變解釋來減少$F$,agent也可以透過改變輸入的感知來優化,意思是agent會去選擇比較符合期待感知輸入,這個也稱為active inference
Agent長期而言希望能最小化surprise,其實就是在最小化Free energy,透過改變自己對於感知輸入的解釋,透過主動選擇感知輸入來源與行為,讓agent能快速的了解適應環境;Free energy 是很有機會做為大腦學習、控制的基礎理論,在 The free-energy principle:a unified brain theory ? 文中有介紹與其他現有理論的關係,像是 Neural coding、Bayesian brain hypothesis 等等
結語
智慧的本質到底是什麼?我們到底是如何快速的學習?又為何要學習?本篇介紹了The free energy principle,我想我們為了要生存,必須要抵抗失序,我們必須讓自己維持在一種認知穩地的狀態,這樣帶來的附加效益就是讓我們有快速的學習能力,最終我們成了一個強大的解釋與預測機器
下一篇會介紹 A tutorial on the free-energy framework for modelling perception and learning 這篇文章,提出一個神經網路的框架能執行基於Free energy principle的計算,相當有趣!敬請期待